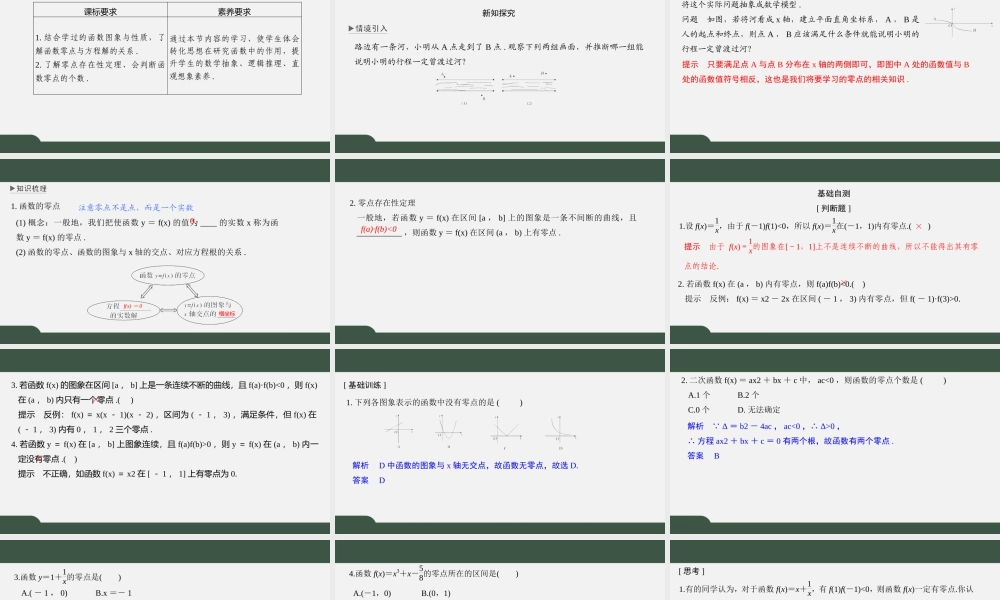
8.1二分法与求方程近似解(第一课时)函数的零点课标要求素养要求1.结合学过的函数图象与性质,了解函数零点与方程解的关系.2.了解零点存在性定理、会判断函数零点的个数.通过本节内容的学习,使学生体会转化思想在研究函数中的作用,提升学生的数学抽象、逻辑推理、直观想象素养.新知探究路边有一条河,小明从A点走到了B点.观察下列两组画面,并推断哪一组能说明小明的行程一定曾渡过河?将这个实际问题抽象成数学模型.问题如图,若将河看成x轴,建立平面直角坐标系,A,B是人的起点和终点,则点A,B应该满足什么条件就能说明小明的行程一定曾渡过河?提示只要满足点A与点B分布在x轴的两侧即可,即图中A处的函数值与B处的函数值符号相反,这也是我们将要学习的零点的相关知识.1.函数的零点注意零点不是点,而是一个实数(1)概念:一般地,我们把使函数y=f(x)的值为____的实数x称为函数y=f(x)的零点.(2)函数的零点、函数的图象与x轴的交点、对应方程根的关系.0f(x)=0横坐标2.零点存在性定理一般地,若函数y=f(x)在区间[a,b]上的图象是一条不间断的曲线,且___________,则函数y=f(x)在区间(a,b)上有零点.f(a)·f(b)<0基础自测[判断题]2.若函数f(x)在(a,b)内有零点,则f(a)f(b)<0.()提示反例:f(x)=x2-2x在区间(-1,3)内有零点,但f(-1)·f(3)>0.1.设f(x)=1x,由于f(-1)f(1)<0,所以f(x)=1x在(-1,1)内有零点.()提示由于f(x)=1x的图象在[-1,1]上不是连续不断的曲线,所以不能得出其有零点的结论.××3.若函数f(x)的图象在区间[a,b]上是一条连续不断的曲线,且f(a)·f(b)<0,则f(x)在(a,b)内只有一个零点.()提示反例:f(x)=x(x-1)(x-2),区间为(-1,3),满足条件,但f(x)在(-1,3)内有0,1,2三个零点.4.若函数y=f(x)在[a,b]上图象连续,且f(a)f(b)>0,则y=f(x)在(a,b)内一定没有零点.()提示不正确,如函数f(x)=x2在[-1,1]上有零点为0.××[基础训练]1.下列各图象表示的函数中没有零点的是()解析D中函数的图象与x轴无交点,故函数无零点,故选D.答案D2.二次函数f(x)=ax2+bx+c中,ac<0,则函数的零点个数是()A.1个B.2个C.0个D.无法确定解析 Δ=b2-4ac,ac<0,∴Δ>0,∴方程ax2+bx+c=0有两个根,故函数有两个零点.答案BA.(-1,0)B.x=-1C.x=1D.x=03.函数y=1+1x的零点是()解析令1+1x=0,则x=-1,故选B.答案B4.函数f(x)=x3+x-58的零点所在的区间是()A.(-1,0)B.(0,1)C.(1,2)D.(-2,-1)解析...