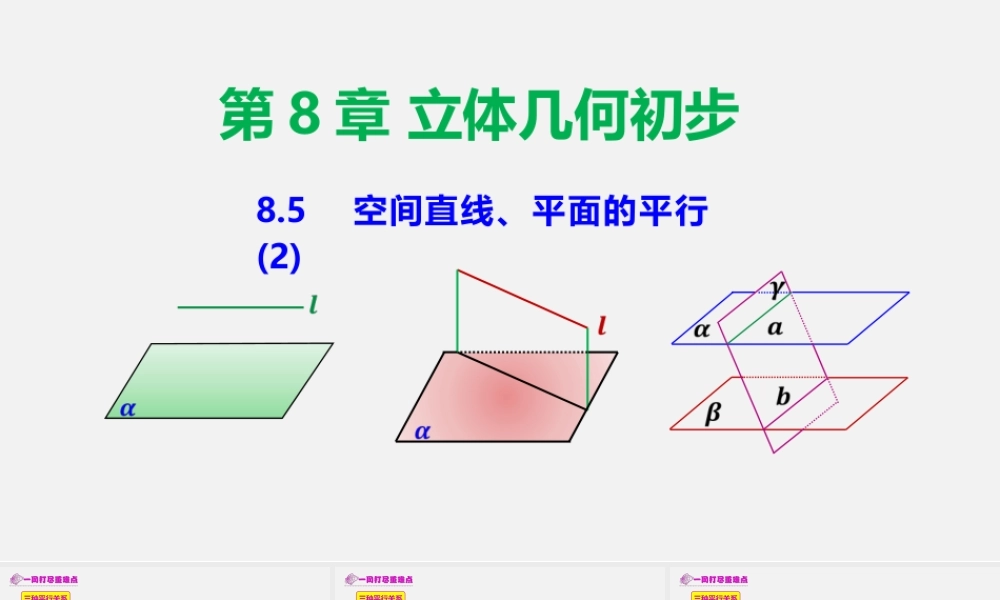
第8章立体几何初步8.5空间直线、平面的平行(2)三种平行关系空间中的平行关系是一种重要的特殊关系,一般以证明题的形式出现,总结如下:线线平行的定义:在同一平面内,永不相交的两条直线叫做平行线平面几何知识:证明共面的两条直线平行.主要有三角形中位线定理;平行四边形的性质;平行线分线段成比例定理;梯形一组对边平行;同位角相等或同旁内角互补两直线平行;向量共线等等【1】直线与直线平行的判定方法三种平行关系空间中的平行关系是一种重要的特殊关系,一般以证明题的形式出现,总结如下:反证法【1】直线与直线平行的判定方法三种平行关系空间中的平行关系是一种重要的特殊关系,一般以证明题的形式出现,总结如下:线面平行的定义:直线与平面没有公共点【2】直线与平面平行的判定方法反证法三种平行关系空间中的平行关系是一种重要的特殊关系,一般以证明题的形式出现,总结如下:面面平行的定义:两个平面没有公共点【3】平面与平面平行的判定方法反证法三种平行关系空间中的平行关系是一种重要的特殊关系,一般以证明题的形式出现,总结如下:【4】三种平行之间的转化关系线面平行线线平行面面平行判定定理判定定理性质定理性质定理判定定理性质定理由左图可以看出,三者之间可以进行适当的转化,即由两条相交直线和平面平行,可以判定两个平面平行,同样由两个平面平行的性质,也可以推出直线和平面平行,直线与直线平行.直线与直线,直线与平面,平面与平面平行的这种相互转化关系,体现了知识间相互依赖的关系正方形ABCD与正方形ABEF所在平面相交于AB,在AE,BD上各有一点P,Q.且AP=DQ,求证:PQ//平面BCE.判定定理条件罗列不全而出错坑①如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PA=AD=1,E,F分别是AB和PD的中点.求证:直线AF//平面PEC.证明平行四边形时忘记四点共面坑②证明平行四边形时忘记四点共面坑②题①——平面基本事实④和等角定理的应用题②——直线与平面平行的判定题③——直线与平面平行的性质题④——平面与平面平行的判定题⑤——平面与平面平行的性质题⑤——平面与平面平行的性质题⑥——线面平行、面面平行的探索性问题THANKS“”