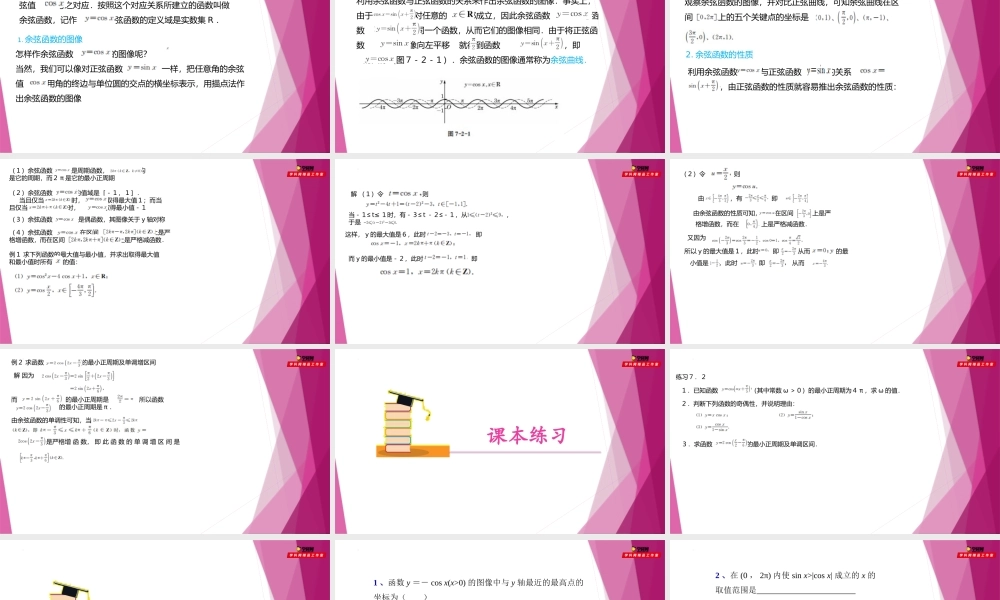
2022-2023学年高一数学同步精品课堂(沪教版2020必修第二册)第7章三角函数7.2余弦函数的图像我们知道,对于任意一个给定的实数,都有唯一确定的余弦值与之对应.按照这个对应关系所建立的函数叫做余弦函数,记作余弦函数的定义域是实数集R.1.余弦函数的图像怎样作余弦函数的图像呢?当然,我们可以像对正弦函数一样,把任意角的余弦值用角的终边与单位圆的交点的横坐标表示,用描点法作出余弦函数的图像但是,由于已经知道了正弦函数的图像,我们可以简便地利用余弦函数与正弦函数的关系来作出余弦函数的图像.事实上,由于对任意的都成立,因此余弦函数与函数是同一个函数,从而它们的图像相同.由于将正弦函数的图像向左平移就得到函数的图像,即的图像(图7-2-1).余弦函数的图像通常称为余弦曲线.观察余弦函数的图像,并对比正弦曲线,可知余弦曲线在区间上的五个关键点的坐标是2.余弦函数的性质利用余弦函数与正弦函数的关系,由正弦函数的性质就容易推出余弦函数的性质:(1)余弦函数是周期函数,均是它的周期,而2π是它的最小正周期(2)余弦函数的值域是[-1,1].当且仅当时,取得最大值1;而当且仅当时,取得最小值-1(3)余弦函数是偶函数,其图像关于y轴对称(4)余弦函数在区间上是严格增函数,而在区间上是严格减函数.例1求下列函数的最大值与最小值,并求出取得最大值和最小值时所有的值:解(1)令,则≤当-1t≤≤1时,有-3t≤-2-1,从而,于是这样,y的最大值是6,此时即而y的最小值是-2,此时即(2)令,则由,有即.由余弦函数的性质可知,在区间上是严格增函数,而在上是严格减函数.又因为所以y的最大值是1,此时即从而的最小值是,此时,即,从而例2求函数的最小正周期及单调增区间解因为而的最小正周期是,所以函数的最小正周期是π.由余弦函数的单调性可知,当是严格增函数,即此函数的单调增区间是课本练习练习7.21.已知函数(其中常数ω>0)的最小正周期为4π,求ω的值.2.判断下列函数的奇偶性,并说明理由:3.求函数的最小正周期及单调区间.随堂检测1、函数y=-cosx(x>0)的图像中与y轴最近的最高点的坐标为()A.B.(π,1)C.(0,1)D.(2π,1)【答案】B;【解析】用五点作图法作出函数y=-cosx(x>0)的一个周期的图像如图所示,由图易知与y轴最近的最高点的坐标为(π,1);2、在(0,2π)内使sinx>|cosx|成立的x的取值范围是【解析】因为,sinx>|cosx|,所...