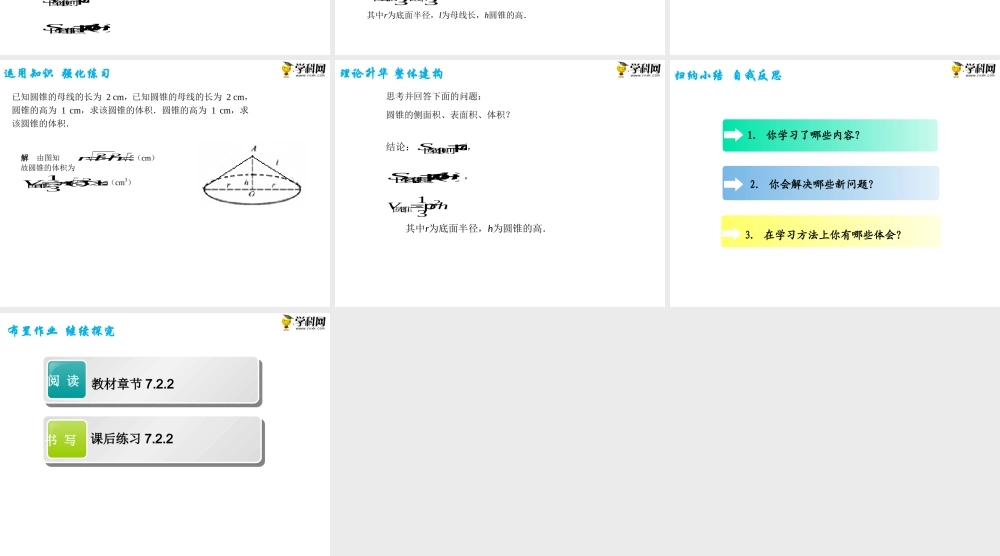
7.2.2圆锥第七章简单几何体创设情境兴趣导入情境与问题如图7-3所示的生活中常见的各种实物,其外形有什么特征?动脑思考探索新知由旋转体的定义,以直角三角形的一条直角边为旋转轴进行旋转,观察旋转一周所形成的几何体(如图7−24).以直角三角形的一条直角边为旋转轴旋转一周,其余各边旋转而形成的几何体叫做圆锥(如图7−24).旋转轴叫做圆锥的轴.另一条直角边旋转而成的圆面叫做底面.斜边旋转而成的曲面叫做侧面,无论旋转到什么位置,斜边都叫做侧面的母线.母线与轴的交点叫做顶点.顶点到底面圆心的距离叫做圆锥的高.动脑思考探索新知观察圆锥,可以得到圆锥的下列性质:(1)平行于底面的截面都是圆;(2)高垂直于底面圆,且过圆心;(3)轴截面为等腰三角形,高为圆锥的高,腰是圆锥的母线,底边是底面圆的直径.动脑思考探索新知沿圆锥体的一条母线将圆锥侧面展开在一个平面上所得的图形称为圆锥的侧面展开图,它是一个扇形,如图7−25所示,这个扇形的面积就是圆锥的侧面积,因为扇形的弧长c是底面圆的周长,扇形的半径l是圆锥的母线的长,所以圆锥的侧面积、表面积为Srl圆锥侧p()Srlr圆锥全p动脑思考探索新知实验圆锥的体积实验用具:等底等高的圆柱和圆锥容器各一个,如图7−26所示,水或细沙.实验步骤:(1)在圆锥容器中装满水或细沙;(2)将圆锥容器中的水或细沙全部倒入圆柱容器中;(3)重复步骤(1)(2)两次.实验结果:水或细沙刚好注满圆柱容器.实验结论:圆柱的体积是等底等高的圆锥体积的3倍.可以证明圆锥的体积为21133VShrh圆锥底p其中r为底面半径,l为母线长,h圆锥的高.巩固知识典型例题例2已知圆柱的轴截面是边长为6cm的等边三角形,求圆锥的表面积与体积.解因为等边三角形的底边和腰分别是圆锥的底面直径和母线,所以圆锥的底面半径2rcm,母线l=4cm,高224223h(cm),故圆锥的表面积为22+==2+24=12SSSrrl表侧底pp(cm2),体积为910=90VSh柱底p(cm3).运用知识强化练习已知圆锥的母线的长为2cm,已知圆锥的母线的长为2cm,圆锥的高为1cm,求该圆锥的体积.圆锥的高为1cm,求该圆锥的体积.解由图知223rlh(cm)故圆锥的体积为21(3)13V圆锥(cm3)理论升华整体建构思考并回答下面的问题:圆锥的侧面积、表面积、体积?结论:Srl圆锥侧p,()Srlr圆锥表p,213Vrh圆锥p,其中r为底面半径,h为圆锥的高.3.在学习方法上你有哪些体会?2.你会...