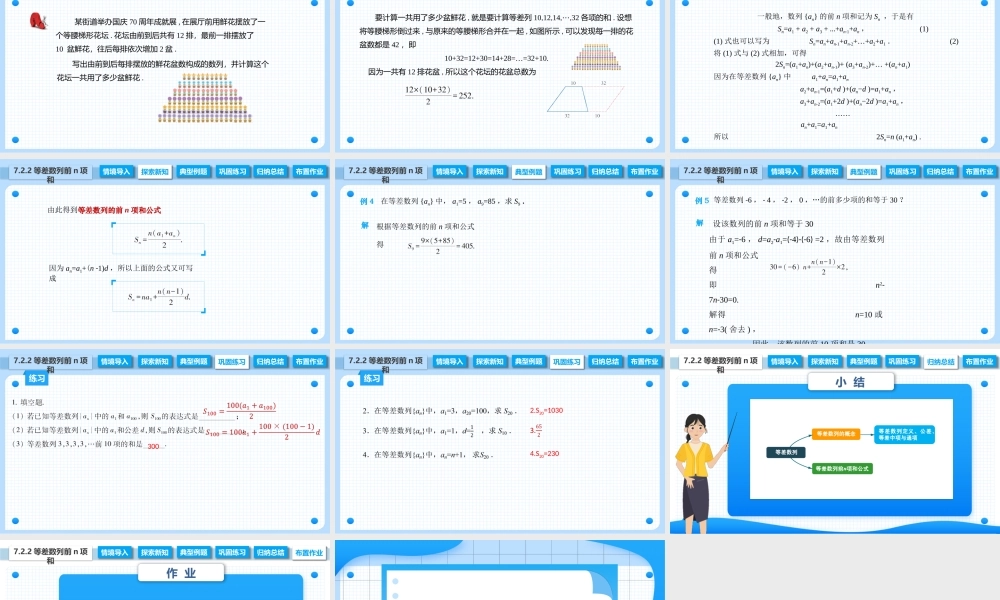
7.2.2等差数列前n项和公式中职数学拓展模块一下册探索新知典型例题巩固练习归纳总结布置作业7.2.2等差数列前n项和情境导入情境导入写出由前到后每排摆放的鲜花盆数构成的数列,并计算这个花坛一共用了多少盆鲜花.某街道举办国庆70周年成就展,在展厅前用鲜花摆放了一个等腰梯形花坛.花坛由前到后共有12排,最前一排摆放了10盆鲜花,往后每排依次增加2盆.探索新知典型例题巩固练习归纳总结布置作业7.2.2等差数列前n项和情境导入情境导入要计算一共用了多少盆鲜花,就是要计算等差列10,12,14,,⋯32各项的和.设想将等腰梯形倒过来,与原来的等腰梯形合并在一起,如图所示,可以发现每一排的花盆数都是42,即10+32=12+30=14+28=…=32+10.因为一共有12排花盆,所以这个花坛的花盆总数为情境导入典型例题巩固练习归纳总结布置作业7.2.2等差数列前n项和情境导入探索新知一般地,数列{an}的前n项和记为Sn,于是有Sn=a1+a2+a3+…+an-1+an,(1)(1)式也可以写为Sn=an+an-1+an-2+…+a2+a1.(2)将(1)式与(2)式相加,可得2Sn=(a1+an)+(a2+an-1)+(a3+an-2)+…+(an+a1)因为在等差数列{an}中a1+an=a1+ana2+an-1=(a1+d)+(an−d)=a1+an,a3+an-2=(a1+2d)+(an−2d)=a1+an,……an+a1=a1+an所以2Sn=n(a1+an).情境导入典型例题巩固练习归纳总结布置作业7.2.2等差数列前n项和情境导入探索新知由此得到等差数列的前n项和公式因为an=a1+(n-1)d,所以上面的公式又可写成例4在等差数列{an}中,a1=5,a9=85,求S9.情境导入典型例题情境导入探索新知巩固练习归纳总结布置作业7.2.2等差数列前n项和解根据等差数列的前n项和公式得例5情境导入典型例题情境导入探索新知巩固练习归纳总结布置作业7.2.2等差数列前n项和等差数列-6,-4,-2,0,…的前多少项的和等于30?解设该数列的前n项和等于30由于a1=-6,d=a2-a1=(-4)-(-6)=2,故由等差数列前n项和公式得即n2-7n-30=0.解得n=10或n=-3(舍去),因此该数列的前10项和是30情境导入巩固练习情境导入探索新知典型例题归纳总结布置作业练习7.2.2等差数列前n项和300情境导入巩固练习情境导入探索新知典型例题归纳总结布置作业练习7.2.2等差数列前n项和2.S20=10304.S20=230情境导入归纳总结情境导入探索新知典型例题巩固练习布置作业7.2.2等差数列前n项和小结情境导入布置作业情境导入探索新知典型例题巩固练习归纳总结7.2.2等差数列前n项和作业1.书面作业:完成教材第64页习题7.2;2.查漏补缺:根据个人情况对课堂学习复习与回顾;3.拓展作业:阅读教材扩展延伸内容.本节课堂结束.教师:姜老师