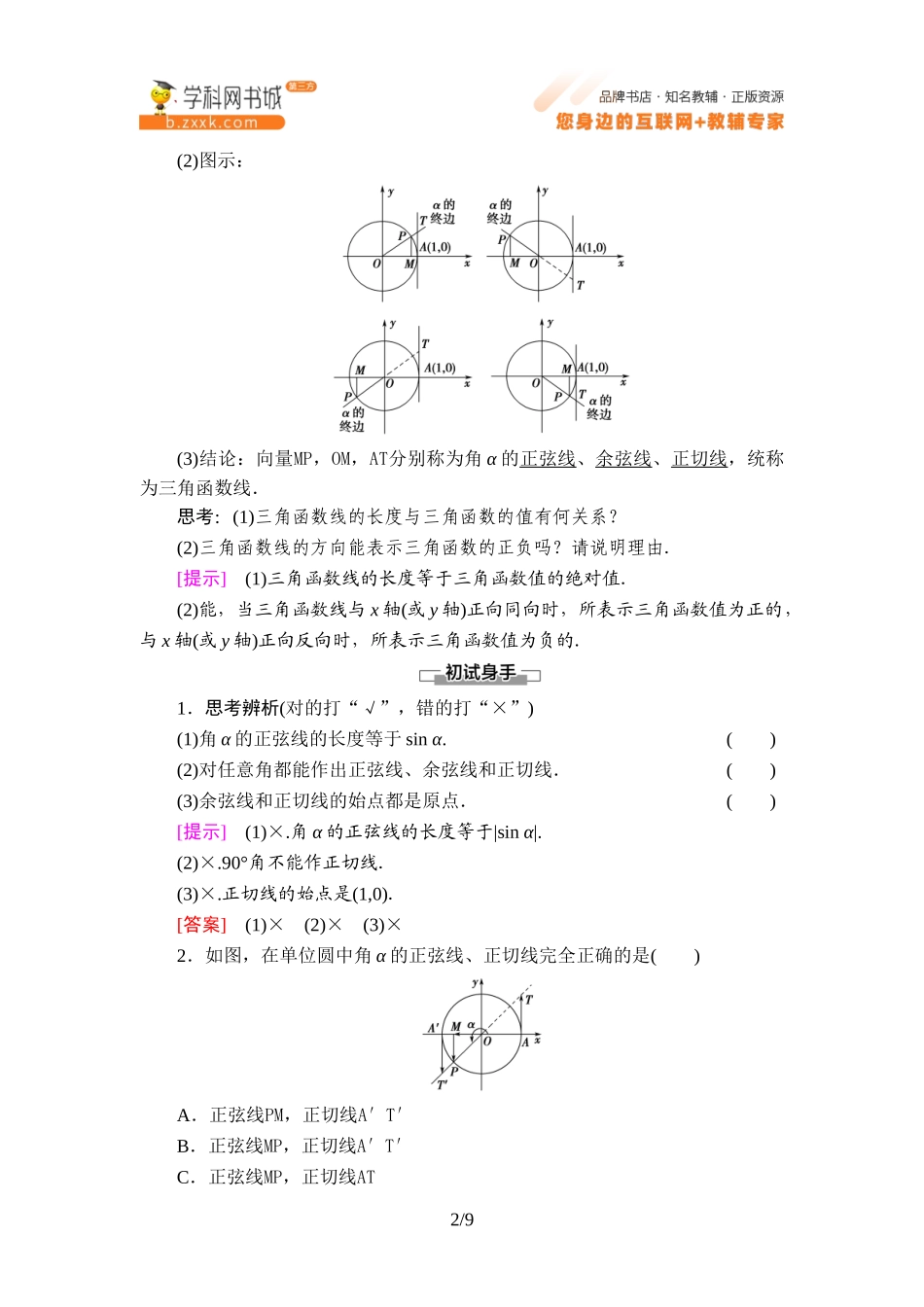
7.2.2单位圆与三角函数线学习目标核心素养1.了解三角函数线的意义,能用三角函数线表示一个角的正弦、余弦和正切.(重点)2.能利用三角函数线解决一些简单的三角函数问题.(难点)1.通过三角函数线概念的学习,培养学生的数学抽象和直观想象核心素养.2.借助三角函数线的应用,培养学生的逻辑推理及直观想象核心素养.江南水乡,水车在清清的河流里悠悠转动,缓缓地把河流里的水倒进水渠,流向绿油油的大地,流向美丽的大自然,在水车转动的瞬间,同学们能想到些什么呢?问题将图中的水车抽象出一个数学模型,建立平面直角坐标系(如图所示),设水车的轮廓为单位圆.在平面直角坐标系中,任意角α的终边与单位圆交于点P,过点P作PM⊥x轴.过点A(1,0)作单位圆的切线,交α的终边或其反向延长线于点T,结合三角函数的定义,你能得到sinα,cosα,tanα与MP,OM,AT的关系吗?提示sinα=MP,cosα=OM,tanα=AT.1.单位圆与三角函数(1)单位圆:在平面直角坐标系中,坐标满足x2+y2=1的点组成的集合.(2)三角函数与单位圆:角α的终边与单位圆相交于点P(x,y),如图:则sinα=y,cosα=x,tanα=,则角α的终边与单位圆的交点为P(cos_α,sin_α).思考:单位圆的圆心和半径分别是什么?[提示]单位圆的圆心在原点,半径为单位长度即半径等于1.2.三角函数线(1)作图:①角α的终边与单位圆交于P,过P作PM垂直于x轴,垂足为M.②过A(1,0)作x轴的垂线,交角α的终边或其反向延长线于点T.1/9(2)图示:(3)结论:向量MP,OM,AT分别称为角α的正弦线、余弦线、正切线,统称为三角函数线.思考:(1)三角函数线的长度与三角函数的值有何关系?(2)三角函数线的方向能表示三角函数的正负吗?请说明理由.[提示](1)三角函数线的长度等于三角函数值的绝对值.(2)能,当三角函数线与x轴(或y轴)正向同向时,所表示三角函数值为正的,与x轴(或y轴)正向反向时,所表示三角函数值为负的.1.思考辨析(对的打“√”,错的打“×”)(1)角α的正弦线的长度等于sinα.()(2)对任意角都能作出正弦线、余弦线和正切线.()(3)余弦线和正切线的始点都是原点.()[提示](1)×.角α的正弦线的长度等于|sinα|.(2)×.90°角不能作正切线.(3)×.正切线的始点是(1,0).[答案](1)×(2)×(3)×2.如图,在单位圆中角α的正弦线、正切线完全正确的是()A.正弦线PM,正切线A′T′B.正弦线MP,正切线A′T′C.正弦线MP,正切线AT2/9D.正弦线PM,正切线ATC[由三角函数线的定义知C正...