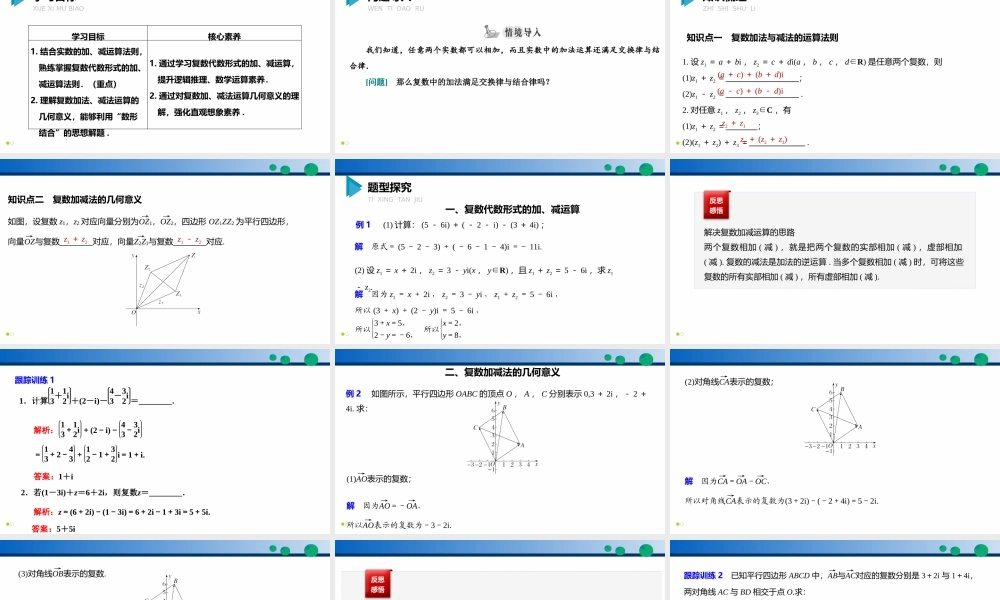
数学7.2.1复数的加、减运算及其几何意义同步精品课件学习目标XUEXIMUBIAO学习目标核心素养1.结合实数的加、减运算法则,熟练掌握复数代数形式的加、减运算法则.(重点)2.理解复数加法、减法运算的几何意义,能够利用“数形结合”的思想解题.1.通过学习复数代数形式的加、减运算,提升逻辑推理、数学运算素养.2.通过对复数加、减法运算几何意义的理解,强化直观想象素养.问题导入WENTIDAORU我们知道,任意两个实数都可以相加,而且实数中的加法运算还满足交换律与结合律.[问题]那么复数中的加法满足交换律与结合律吗?知识梳理ZHISHISHULI知识点一复数加法与减法的运算法则1.设z1=a+bi,z2=c+di(a,b,c,d∈R)是任意两个复数,则(1)z1+z2=;(2)z1-z2=.2.对任意z1,z2,z3∈C,有(1)z1+z2=;(2)(z1+z2)+z3=.(a+c)+(b+d)i(a-c)+(b-d)iz2+z1z1+(z2+z3)知识点二复数加减法的几何意义如图,设复数z1,z2对应向量分别为OZ1→,OZ2→,四边形OZ1ZZ2为平行四边形,向量OZ→与复数对应,向量Z2Z1→与复数对应.z1+z2z1-z2题型探究TIXINGTANJIU例1(1)计算:(5-6i)+(-2-i)-(3+4i);一、复数代数形式的加、减运算所以3+x=5,2-y=-6,所以x=2,y=8,解原式=(5-2-3)+(-6-1-4)i=-11i.(2)设z1=x+2i,z2=3-yi(x,y∈R),且z1+z2=5-6i,求z1-z2.解因为z1=x+2i,z2=3-yi,z1+z2=5-6i,所以(3+x)+(2-y)i=5-6i,反思感悟解决复数加减运算的思路两个复数相加(减),就是把两个复数的实部相加(减),虚部相加(减).复数的减法是加法的逆运算.当多个复数相加(减)时,可将这些复数的所有实部相加(减),所有虚部相加(减).跟踪训练1解析:z=(6+2i)-(1-3i)=6+2i-1+3i=5+5i.答案:5+5i1.计算13+12i+(2-i)-43-32i=________.解析:13+12i+(2-i)-43-32i=13+2-43+12-1+32i=1+i.答案:1+i2.若(1-3i)+z=6+2i,则复数z=________.二、复数加减法的几何意义解因为AO→=-OA→,例2如图所示,平行四边形OABC的顶点O,A,C分别表示0,3+2i,-2+4i.求:(1)AO→表示的复数;所以AO→表示的复数为-3-2i.解因为CA→=OA→-OC→,(2)对角线CA→表示的复数;所以对角线CA→表示的复数为(3+2i)-(-2+4i)=5-2i.解因为OB→=OA→+OC→,(3)对角线OB→表示的复数.所以对角线OB→表示的复数为(3+2i)+(...