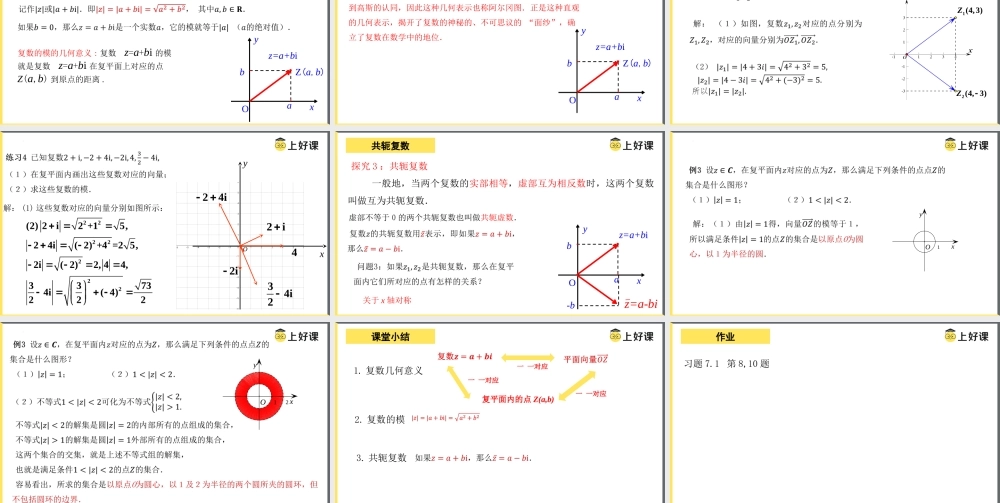
人教A版数学必修二7.1.2复数的几何意义3.复数相等的充要条件在复数集C={a+bi|a,b∈R}中任取两个数a+bi,c+di(a,b,c,d∈R),规定a+bi与c+di相等当且仅当__________________.1.复数的定义我们把形如a+bi(a,b∈R)的数叫做复数,其中i叫做__________,满足i2=___.全体复数所构成的集合C=______________叫做复数集.2.复数的表示复数通常用字母z表示,即z=a+bi(a,b∈R),其中的a与b分别叫做复数z的______与_______.虚数单位-1{a+bi|a,b∈R}实部虚部a=c且b=d复习回顾探究1:复数的几何意义我们知道,实数与数轴上的点一一对应,因此实数可以用数轴上的点来表示.复数有什么几何意义呢?复数的几何意义xo1实数数轴上的点(数)一一对应(形)复数的几何意义复数集与平面直角坐标系中的点集之间可以建立一一对应关系.一一对应一一对应平面直角坐标系中的点一一对应复平面一一对应一一对应复平面内的点Z(a,b)一一对应xy0Z(a,b)abz=a+biiZ()zaba,b一一对应复数复平面内的点实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.复数的几何意义练习2说出图中复平面内各点所表示的复数(每个小方格的边长为1).43i33i32i33i525i5iOxy25i32i24i3i53i问题2:在平面直角坐标系中,每一个平面向量都可以用一个有序实数对来表示,而有序实数对与复数是一一对应的.你能用平面向量来表示复数吗?yZxo一一对应一一对应一一对应实数0与零向量对应复数的几何意义一一对应一一对应一一对应复平面内的点Z(a,b)一一对应xyOZ(a,b)abz=a+bi复数的几何意义xyOZ(a,b)abz=a+bi复数的模的几何意义:复数z=a+bi的模就是复数z=a+bi在复平面上对应的点Z(a,b)到原点的距离.复数的模注:在本书的第六章,我们提到复数的这种几何表示是由韦塞尔在1797年提出的.后来,阿尔冈出书对此进行讨论,并得到高斯的认同,因此这种几何表示也称阿尔冈图.正是这种直观的几何表示,揭开了复数的神秘的、不可思议的“面纱”,确立了复数在数学中的地位.xyOZ(a,b)abz=a+bi课外补充1(4,3)Z2(4,3)Z解:(1)这些复数对应的向量分别如图所示:2222222(2)2i2+15,24i(2)+4=25,2i(2)2,44,33734i(4)222Oxy2i24i2i434i2探究3:共轭复数一般地,当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数.虚部不等于0的两个共轭复数也叫做共轭虚数.z=a-bixyOabz=a+bi-b关于x轴对称共轭复数xy1Oxy21O1.复数几何意义2.复数的模3.共轭复数课堂小结一一对应一一对应复平面内的点Z(a,b)一一对应作业习题7.1第8,10题