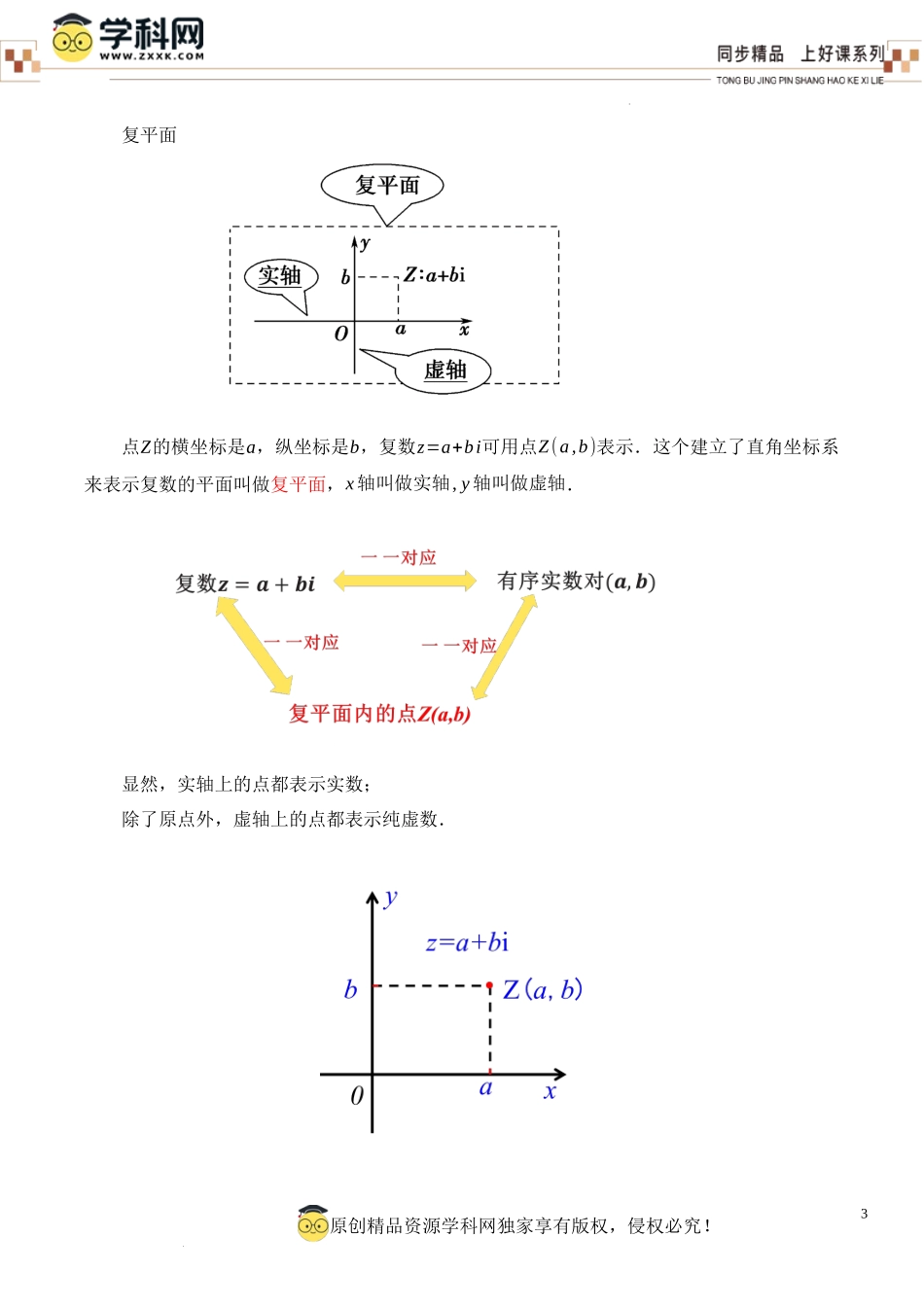
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司7.1.2复数的几何意义教学设计一、教学目标1.理解可以用复平面内的点和向量来表示复数及它们之间的一一对应关系;2.掌握实轴、虚轴、模等概念以及用向量的模来表示复数的模的方法.3.通过对复数的几何意义的学习,培养学生数学抽象、数学运算、数学建模等数学素养.二、教学重难点1.教学重点:理解复数的几何意义;2.教学难点:根据复数的代数形式描出其对应的点及求复数的模和有关模的运算.三、教学过程1、复习引入(1)复数的定义我们把形如z=a+bi,(a,b∈R)的数叫做复数,其中i叫做虚数单位,满足i2=−1.全体复数所构成的集合C={a+bi∨a,b∈R}叫做复数集.(2)复数的表示复数通常用字母z表示,即z=a+bi,(a,b∈R),其中的a与b分别叫做复数z的实部与虚部.复数相等的充要条件在复数集C={a+bi∨a,b∈R}中任取两个数a+bi,c+di(a,b,c,d∈R),规定a+bi与c+di相等当且仅当a=c,b=d.2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司【设计意图】通过复习已经学过的知识,引出新的知识点,帮助学生更好地理解和掌握新的概念和技能.这种引入方式有助于学生在原有知识的基础上,自然地过渡到新的学习内容.2、新知探索探究1:复数的几何意义我们知道,实数与数轴上的点一一对应,因此实数可以用数轴上的点来表示.复数有什么几何意义呢?问题1:根据复数相等的定义,任何一个复数z=a+bi都可以由一个有序实数对(a,b)唯一确定;反之也对.由此你能想到复数的几何表示方法吗?复数集与平面直角坐标系中的点集之间可以建立一一对应关系.3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司复平面点Z的横坐标是a,纵坐标是b,复数z=a+bi可用点Z(a,b)表示.这个建立了直角坐标系来表示复数的平面叫做复平面,x轴叫做实轴,y轴叫做虚轴.显然,实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.4原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司iZ()zaba,b一一对应复数复平面内的点【设计意图】图像可以直观地展现出数学概念和性质,使得抽象的数学概念变得更易于理解和掌握.练习1:复平面内的原点(0,0)表示实数0,实轴上的点(2,0)表示实数2,虚轴上的点(0,−1)表示纯虚数−i,点(−2,3)表示复数−2+3i等.练习2:说出图中复平面内各点所表示的复数(每个小方格的边长为1).练习3在复平面内,描...