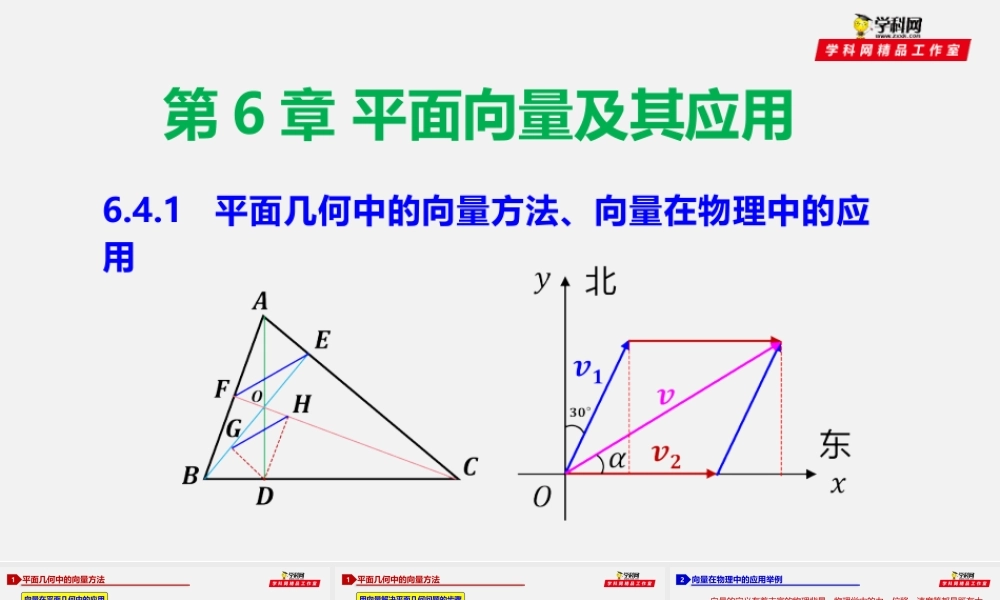
第6章平面向量及其应用6.4.1平面几何中的向量方法、向量在物理中的应用平面几何中的向量方法1向量在平面几何中的应用平面向量在平面几何中的应用主要是用向量的线性运算及数量积解决平面几何中的平行、垂直、长度、夹角问题.(4)求线段长度或证明线段相等问题,利用向量模的公式:平面几何中的向量方法1用向量解决平面几何问题的步骤建立平面几何与向量的关系,用向量表示问题中涉及到的几何元素,将平面几何问题转化为向量问题通过向量运算,研究几何元素之间的关系,如距离、夹角等等把运算结果“翻译”成几何关系.用向量研究几何问题的思想——向量集数与形于一身,既有代数的抽象性,又有几何的直观性,用向量解决平面几何的问题,就是把几何中的“证”,转化为向量的“算”,思路清晰,便于操作.向量在物理中的应用举例2向量的定义有着丰富的物理背景,物理学中的力、位移、速度等都是既有大小又有方向的量,力所做的功就是向量数量积的物理背景.因此,利用向量可以方便地解决一些物理问题.力学问题的向量处理方法解决此类问题必须用向量知识将力学问题转化为数学问题,即将力学各量之间的关系抽象成数学模型,再利用这个模型来解析回答相关物理现象.12向量是既有大小又有方向的量,表示向量的有向线段可以有共同的起点,也可以没有共同的起点.力是既有大小又有方向的量,用向量知识解决共点力的问题,往往需要把向量平移到同一作用点上.向量在物理中的应用举例2向量的定义有着丰富的物理背景,物理学中的力、位移、速度、等都是既有大小又有方向的量,力所做的功就是向量数量积的物理背景.因此,利用向量可以方便的解决一些物理问题.速度、位移问题的向量处理方法速度、加速度与位移的合成和分解,实质就是向量的加减运算,而运动的叠加也用到了向量的合成12向量在速度、加速度上的应用,实质是通过向量的线性运算解决物理问题,从而获得物理结果.用向量解决速度、加速度和位移问题,用的只是主要是向量的加法、减法以及数乘,有时也可以利用坐标来解决.向量在物理中的应用举例2总结——向量解决平面几何问题的两种方法【基底法】选取适当的基底(尽量选取已知模长或夹角的向量作为基底),将题中涉及的向量用基底表示,利用向量的运算法则、运算规律及相关结论来探究几何关系.【坐标法】建立平面直角坐标系,实现几何关系的向量化、坐标化,从而将几何问题代数化.一般地,存在坐标系或者便于建立坐标系的题型适合用坐标法.力、速度和加速度一样...