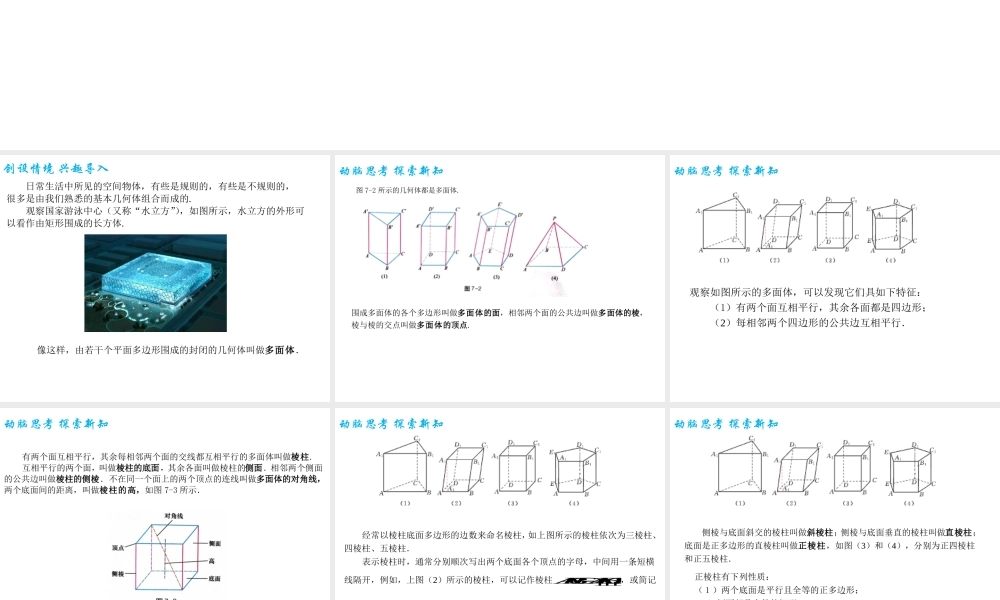
7.1.1棱柱第七章简单几何体创设情境兴趣导入日常生活中所见的空间物体,有些是规则的,有些是不规则的,很多是由我们熟悉的基本几何体组合而成的.观察国家游泳中心(又称“水立方”),如图所示,水立方的外形可以看作由矩形围成的长方体.像这样,由若干个平面多边形围成的封闭的几何体叫做多面体.动脑思考探索新知图7-2所示的几何体都是多面体.围成多面体的各个多边形叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的交点叫做多面体的顶点.动脑思考探索新知观察如图所示的多面体,可以发现它们具如下特征:(1)有两个面互相平行,其余各面都是四边形;(2)每相邻两个四边形的公共边互相平行.有两个面互相平行,其余每相邻两个面的交线都互相平行的多面体叫做棱柱.互相平行的两个面,叫做棱柱的底面,其余各面叫做棱柱的侧面.相邻两个侧面的公共边叫做棱柱的侧棱.不在同一个面上的两个顶点的连线叫做多面体的对角线,两个底面间的距离,叫做棱柱的高,如图7-3所示.动脑思考探索新知动脑思考探索新知经常以棱柱底面多边形的边数来命名棱柱,如上图所示的棱柱依次为三棱柱、四棱柱、五棱柱.表示棱柱时,通常分别顺次写出两个底面各个顶点的字母,中间用一条短横线隔开,例如,上图(2)所示的棱柱,可以记作棱柱1111ABCDABCD,或简记作棱柱1AC.动脑思考探索新知侧棱与底面斜交的棱柱叫做斜棱柱;侧棱与底面垂直的棱柱叫做直棱柱;底面是正多边形的直棱柱叫做正棱柱,如图(3)和(4),分别为正四棱柱和正五棱柱.正棱柱有下列性质:(1)两个底面是平行且全等的正多边形;(2)侧面都是全等的矩形;(3)侧棱互相平行并垂直于底面,各侧棱长都相等,并且等于正棱柱的高.动脑思考探索新知将棱柱的侧面沿一条侧棱展开在一个平面上所得到的图形称为棱柱的侧面展开图.侧面展开图的面积称为棱柱的侧面积,因为直棱柱的侧面展开图是矩形,它的上、下两条对边长等于直棱柱的底面周长c,另两条对边长等于直棱柱的高h,如图7-4所示.所以直棱柱侧面积为Sch直棱柱侧直棱柱的侧面积与两个底面面积之和,叫做直棱柱的表面积或全面积.直棱柱的表面积为2SchS直棱柱表底可以证明直棱柱的体积计算公式为VSh直棱柱底其中,底S表示直棱柱的底面的面积,c是表示直棱柱的底面周长,h是直棱柱的高.巩固知识典型例题例1已知一个正四棱柱的底面边长为2cm,高为3cm,求这个正四棱柱的全面积和体积.解正四棱柱的全面积为S全=2chS底=(2...