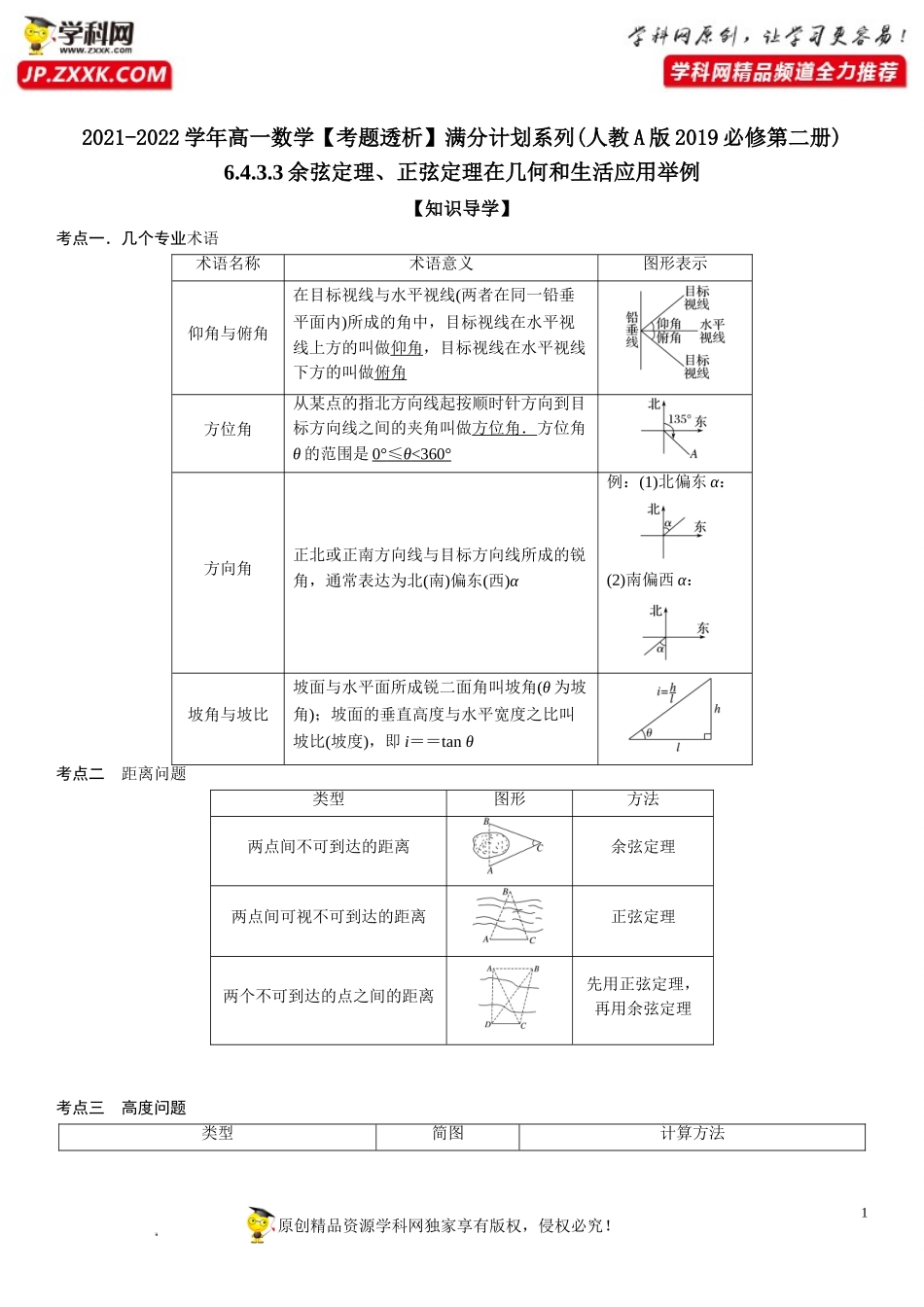
12021-2022学年高一数学【考题透析】满分计划系列(人教A版2019必修第二册)6.4.3.3余弦定理、正弦定理在几何和生活应用举例【知识导学】考点一.几个专业术语术语名称术语意义图形表示仰角与俯角在目标视线与水平视线(两者在同一铅垂平面内)所成的角中,目标视线在水平视线上方的叫做仰角,目标视线在水平视线下方的叫做俯角方位角从某点的指北方向线起按顺时针方向到目标方向线之间的夹角叫做方位角.方位角θ的范围是0°≤θ<360°方向角正北或正南方向线与目标方向线所成的锐角,通常表达为北(南)偏东(西)α例:(1)北偏东α:(2)南偏西α:坡角与坡比坡面与水平面所成锐二面角叫坡角(θ为坡角);坡面的垂直高度与水平宽度之比叫坡比(坡度),即i==tanθ考点二距离问题类型图形方法两点间不可到达的距离余弦定理两点间可视不可到达的距离正弦定理两个不可到达的点之间的距离先用正弦定理,再用余弦定理考点三高度问题类型简图计算方法原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司2底部可达测得BC=a,∠BCA=C,AB=a·tanC.底部不可达点B与C,D共线测得CD=a及C与∠ADB的度数.先由正弦定理求出AC或AD,再解三角形得AB的值.点B与C,D不共线测得CD=a及∠BCD,∠BDC,∠ACB的度数.在△BCD中由正弦定理求得BC,再解三角形得AB的值.【考题透析】透析题组一:正、余弦定理判定三角形的形状问题1.(2021·浙江·杭州市富阳区场口中学高一阶段练习)在中,若,,则形状为()A.直角三角形B.等腰三角形C.等边三角形D.等腰直角三角形2.(2021·上海·高一专题练习)已知的三个内角所对的边分别为,满足,且,则的形状为A.等边三角形B.等腰直角三角形C.顶角为的等腰三角形D.顶角为的等腰三角形3.(2020·贵州铜仁伟才学校高一期中)对于,有如下四个命题:①若,则为等腰三角形,②若,则是直角三角形③若,则是钝角三角形④若,则是等边三角形.其中正确的命题个数是A.B.C.D.原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司学科网(北京)股份有限公司3透析题组二:求三角形的周长或者边长最值或范围问题4.(2021·天津经济技术开发区第一中学高一期中)在锐角三角形ABC中,若,且满足关系式,则的取值范围是()A.B.C.D.5.(2021·全国·高一期末)中,角、、的对边分别为、、,且,若的面积为,则的最小值为()A.B.C.D.6.(2020·新疆·乌鲁木齐...