6.4.3.2 正弦定理（备课件）-【上好课】2021-2022学年高一数学同步备课系列（人教A版2019必修第二册）.pptxVIP免费

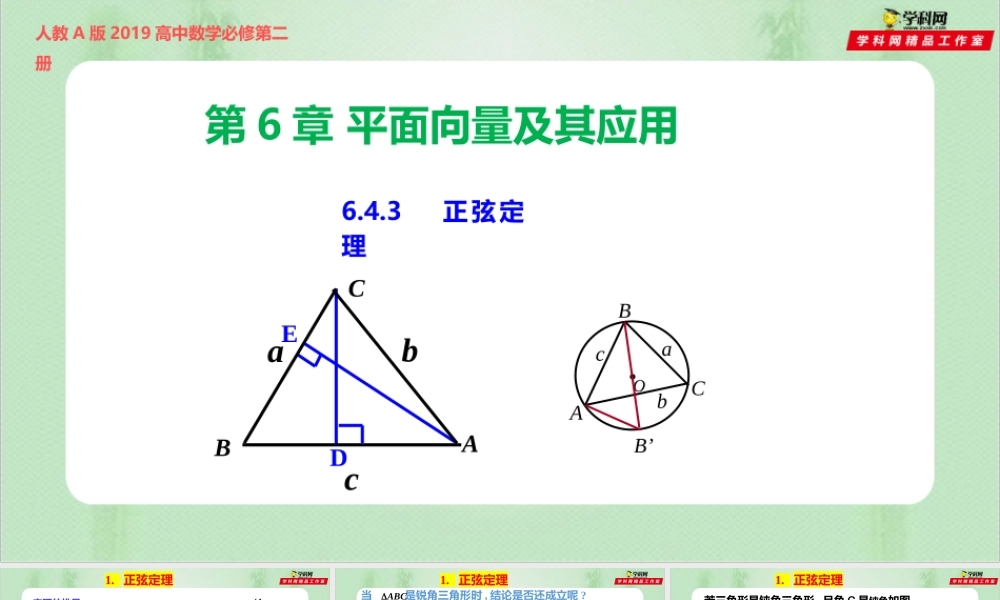
人教A版2019高中数学必修第二册第6章平面向量及其应用6.4.3正弦定理DBACabcE.OACBabcB’1.正弦定理1.定理的推导回忆一下直角三角形的边角关系?ABCcba两等式间有联系吗？sinsinabcABsin1CsinsinsinabcABC思考:对一般的三角形,这个结论还能成立吗?caAsincbBsin1.正弦定理当是锐角三角形时,结论是否还成立呢?ABCD如图:作AB上的高是CD,根椐三角形的定义,得到.sinsinbcAEBCBC同理,作有sin,sinCDaBCDbAsinsinaBbA所以sinsinabAB得到BACabcEsinsinsinabcABC1.正弦定理CbADCsinsin）（且CcBbsinsinD若三角形是钝角三角形,且角C是钝角如图2,此时也有cADBsin交BC延长线于D,过点A作ADBC⊥，CAcbB图2所以AD=csinB=bsinC,即csinsinaAC同理可得sinsinsinabcABCa1.正弦定理在△ABC中,已知BC=a,AC=b,AB=c.作△ABC的外接圆，O为圆心，连接BO并延长交圆于B’，设BB’=2R.则根据直径所对的圆周角是直角以及同弧所对圆周角相等可以得到:,90'BAB'CB，RcBC2'sinsin2sincRC，RBbRAa2sin,2sin同理可得.2sinsinsin成立等式RCcBbAa.OACBabcB’正弦定理的描述在一个三角形中，各边的长度和它所对的角的正弦的比相等1.适用范围：任意的三角形2.简单应用：实现三角形中边角关系的转化1.正弦定理对正弦定理，还有其他证明方法吗?教材中给出了当ΔABC为直角三角形时正弦定理的证明，现在我们给出当ΔABC为钝角三角形时的证明向量法证明正弦定理2.正弦定理的推论：2sinsinsinabcRABC其中，R是△ABC的外接圆的半径公式变形：a=_______，b=________，c=________2RsinA2RsinB2RsinCsin____,sin____,sin____ABC2aR2bR2cRsinA>sinB>sinCABCabc特别地：“边角互化”拓展：任意△ABC中，a:b:c=_________________sinA:sinB:sinC正弦定理可用于两类解三角形：（1）已知两个角一边，求其他两边与另一角；（2）已知两边与一边的对角，计算其他的角与边.（可能会有多解）3.正弦定理的应用典例分析题型1两个角一边，求其他两边与另一角例1：在△ABC中，已知c=10,A=45。,C=30。，求a.BACbca解：105)(180180CABCBAsinsinsinabcABC又sin10sin45=102sinsin30cAaC除了可以求a，你还能求出哪些量？试一试典例分析CAacBbABC,,1,60,320和求，中：在例典例分析解：231630sin316sinsinaAbBＢ＝60°,或Ｂ＝120°当时Ｂ＝60...