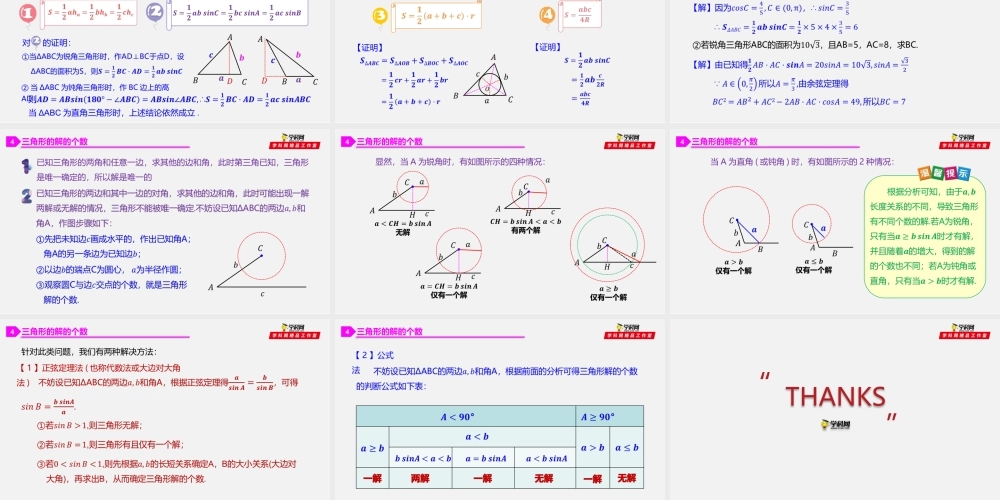
第6章平面向量及其应用6.4.3正弦定理正弦定理1正弦定理的描述【文字语言】在一个三角形中,各边的长度和它所对的角的正弦的比相等适用范围:任意的三角形结构特征:分式连等形式,各边与其对角的正弦严格对应,体现了数学的对称之美.简单应用:实现三角形中边角关系的转化正弦定理1正弦定理的应用已知两角和任一边,求其他的边和角——考什么已知两边和其中一边的对角,求其他边和角——怎么考作为知识形态,放在选择题,填空题中考大题考察正弦定理,常与三角函数,三角恒等变换结合,考察工具形态边角互相转化正弦定理1正弦定理的证明【证法1】定义法(利用三角函数的定义)教材中给出了当ΔABC为直角三角形时正弦定理的证明,现在我们给出当ΔABC为钝角三角形时的证明如图,设∠ABC为钝角,过点C作AB的垂线与AB的延长线交于点D.正弦定理1正弦定理的证明【证法2】向量法(利用向量的数量积定义)教材中给出了当ΔABC为直角三角形时正弦定理的证明,现在我们给出当ΔABC为钝角三角形时的证明下列有关正弦定理的叙述:【解】正弦定理适用于人以三角形,故①②不正确;正弦定理1三角形中的隐含条件即在锐角三角形中,一个角的正弦值大于另一个角的余弦值.正弦定理1正弦定理的推广及常用变形公式利用正弦定理解三角形的类型及方法2类型已知条件一般解法已知三角形的两角和任意一边已知三角形的两边和其中一边的对角解的个数不唯一①应用正弦定理解三角形时,必须明确三角形中边角之间的对应关系;②已知两边和其中一边的对角解三角形时,解的个数不唯一确定,需要讨论;③解三角形时,要注意大边对大角这一性质的运用.解决几何问题的常见公式3三角形的高当ΔABC为直角三角形或钝角三角形时结论相同.解决几何问题的常见公式3三角形面积的计算公式对的证明:②当ΔABC为钝角三角形时,作BC边上的高AD,当ΔABC为直角三角形时,上述结论依然成立.解决几何问题的常见公式3三角形面积的计算公式【证明】【证明】三角形的解的个数4已知三角形的两角和任意一边,求其他的边和角,此时第三角已知,三角形是唯一确定的,所以解是唯一的三角形的解的个数4显然,当A为锐角时,有如图所示的四种情况:三角形的解的个数4当A为直角(或钝角)时,有如图所示的2种情况:三角形的解的个数4针对此类问题,我们有两种解决方法:【1】正弦定理法(也称代数法或大边对大角法)三角形的解的个数4【2】公式法一解一解两解无解一解无解THANKS“”