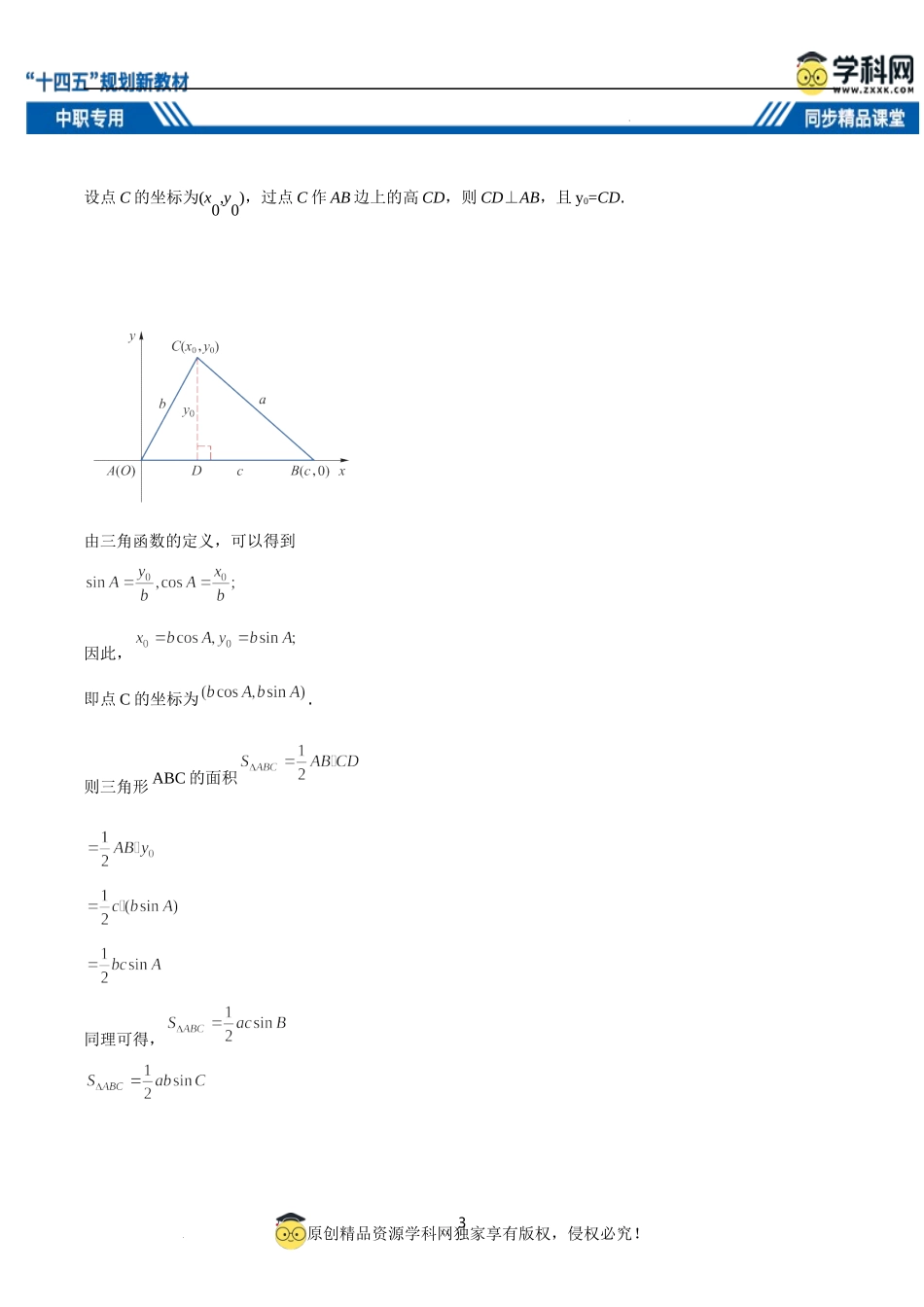
1原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司6.4.1三角形面积公式学习目标学习重难点教材分析通过初中所学的面积公式推导高中的三角形面积公式,这组公式有更高的灵活性.学情分析学生在初中已学过了三角形的面积公式,有了一定的基础,但推导过程较为复杂,学生理解起来比较困难,需要注意.教学工具教学课件知识能力与素养熟记三角形面积公式,能运用公式解决问题.通过推导三角形面积公式将几何问题转化为代数问题,培养转化、化归的数学思想.重点难点利用三角形面积公式解三角形.三角形面积公式的应用.2原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司课时安排1课时教学过程6.4解三角形ΔABC中,常用∠A、∠B、∠C表示三个角,用a、b、c分别表示这三个角的对边.根据已知条件求三角形的边和角的过程称为解三角形.在生产实践和科学研究中,经常会遇到解三角形的问题.余弦定理和正弦定理反映了任意三角形中边和角之间的数量关系,是解三角形的重要工具.6.4.1三角形面积公式(一)创设情境,生成问题为迎接国庆节,某职业学校对校园重新进行修整.园林工人计划利用一夹角成60°的墙角修建一个三角形花圃(如图).若墙角的两面墙的长度分别为4m和6m,问所建花圃的面积是多少平方米(不考虑其他因素)?【设计意图】通过具体实例构造数学模型.(二)调动思维,探究新知用ΔABC表示所建花圃,其中,b=4,c=6.以ΔABC的顶点A为坐标原点,建立如图所示的平面直角坐标系.于是,点A的坐标为(0,0),点B的坐标为(c,0).3原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司设点C的坐标为(x0,y0),过点C作AB边上的高CD,则CD⊥AB,且y0=CD.由三角函数的定义,可以得到因此,即点C的坐标为.则三角形ABC的面积同理可得,4原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司因此,这就是说,三角形的面积等于它的任意两边及其夹角的正弦乘积的一半.【设计意图】根据已学三角形面积公式及三角函数定义推导三角形面积公式,体会数形结合思想.(三)巩固知识,典例练习【典例1】在ΔABC中,∠C=60°,b=6,a=4,求SABC△的值.解:由三角形的面积公式可得,通过本题的计算可知,“情境与问题”中花圃的面积为.【设计意图】例1是对三角形面积公式的具体应用.【典例2】在ΔABC中,解:由三角形面积公式可得,于是即5原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份...