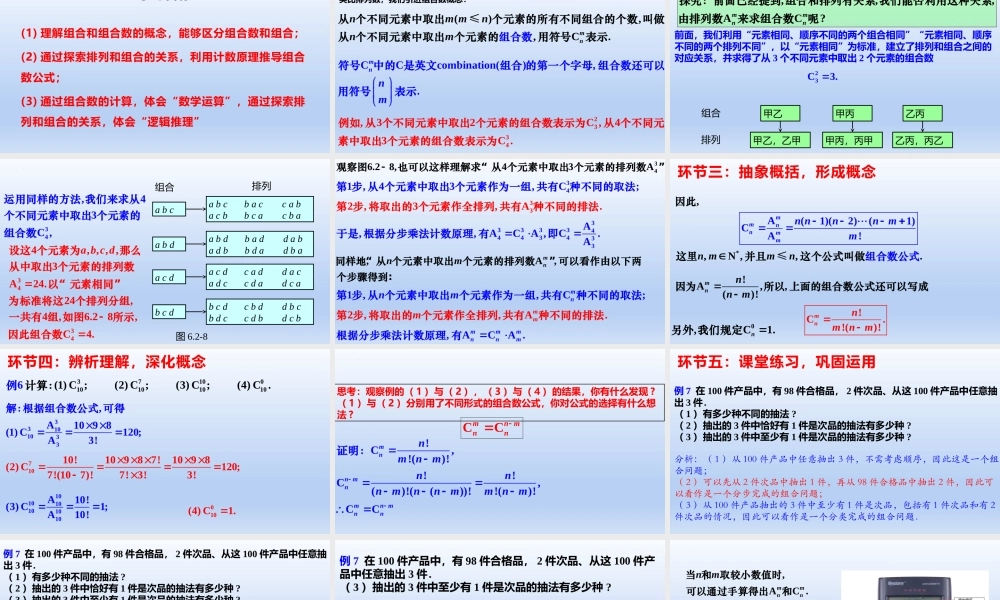
人教A版2019选择性必修第三册(1)理解组合和组合数的概念,能够区分组合数和组合;(2)通过探索排列和组合的关系,利用计数原理推导组合数公式;(3)通过组合数的计算,体会“数学运算”,通过探索排列和组合的关系,体会“逻辑推理”学习目标类比排列数,我们引进组合数概念:,,.()Cmnmmnnnm从个不同元素中取出个元素的所有不同组合的个数叫组合数做从个不同元素中取出个元素的用符号表示≤CCcombination(),.mnnm符号中的是英文组合的第一个字母组合数还可以用符号表示2334,32C,43C.例如从个不同元素中取出个元素的组合数表示为从个不同元素中取出个元素的组合数表示为环节一:创设情境,引入课题,,,?ACmmnn探究:前面已经提到组合和排列有关系我们能否利用这种关系由排列数来求组合数呢前面,我们利用“元素相同、顺序不同的两个组合相同”“元素相同、顺序不同的两个排列不同”,以“元素相同”为标准,建立了排列和组合之间的对应关系,并求得了从3个不同元素中取出2个元素的组合数23C3.甲乙甲丙甲乙,乙甲甲丙,丙甲乙丙乙丙,丙乙组合排列环节二:观察分析,感知概念abcabcbaccabacbbcacbaabdabdbaddabadbbdadbaacdacdcaddacadccdadcabcdbcdcbddbcbdccdbdcb图6.2-8组合排列34,43C,运用同样的方法我们来求从个不同元素中取出个元素的组合数34344,,,,3A24.24,4,6.28,C4.abcd设这个元素为那么从中取出个元素的排列数以“元素相同”为标准将这个排列分组一共有组如图所示因此组合数346.28,43A观察图也可以这样理解求“从个元素中取出个元素的排列数”341,43,C;第步从个元素中取出个元素作为一组共有种不同的取法332,3,A.第步将取出的个元素作全排列共有种不同的排法333334443433A,,ACA,C.A于是根据分步乘法计数原理有即A,,mnnm同样地“从个元素中取出个元素的排列数”可以看作由以下两个步骤得到:1,,C;mnnm第步从个元素中取出个元素作为一组共有种不同的取法2,,A.mmm第步将取出的个元素作全排列共有种不同的排法,ACA.mmmnnm根据分步乘法计数原理有*A(1)(2)(1,,N,)A!,C.mmnnmmnnnnnmnmmm这里这个公式叫组合因此并做且数公式≤!A,,!C.!()!()!mnnmnnmnnmm上面的组合数公式还可以写成因为所以0,C1.n另外我们规定环节三:抽象概括,形成概念3710010101010(1)C;(2)C;(3)C;(4)C6.计例算:33101033,A1098(1)C120;A3!解:根据组合数公式可得71010!10987!1098(2)C120;7!(107)!7!3!3!...