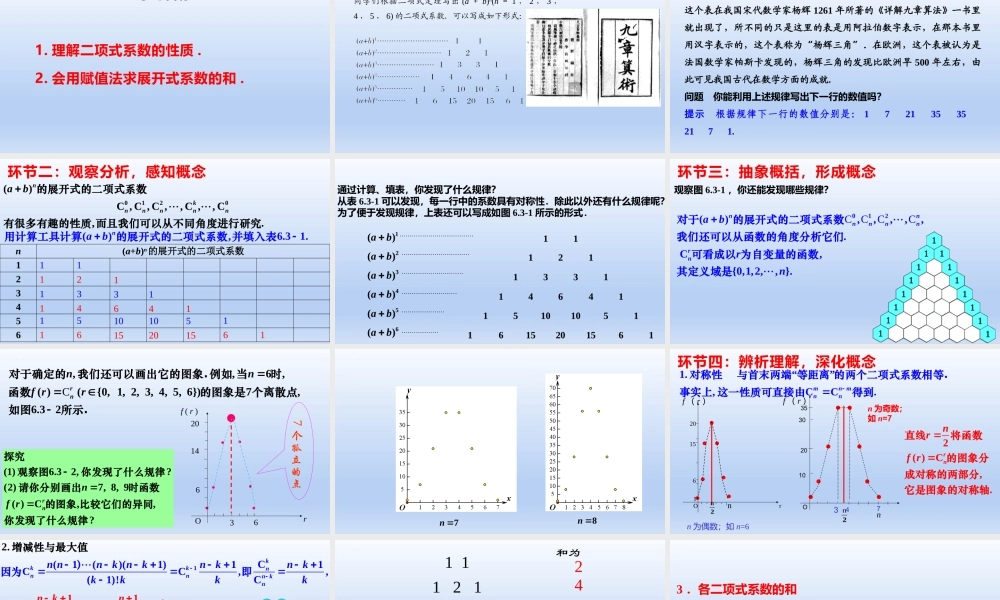
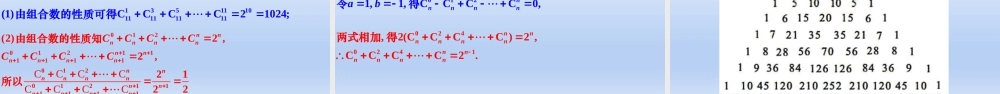人教A版2019选择性必修第三册1.理解二项式系数的性质.2.会用赋值法求展开式系数的和.学习目标同学们根据二项式定理写出(a+b)n(n=1,2,3,4,5,6)的二项式系数.可以写成如下形式:环节一:创设情境,引入课题这个表在我国宋代数学家杨辉1261年所著的《详解九章算法》一书里就出现了,所不同的只是这里的表是用阿拉伯数字表示,在那本书里用汉字表示的,这个表称为“杨辉三角”.在欧洲,这个表被认为是法国数学家帕斯卡发现的,杨辉三角的发现比欧洲早500年左右,由此可见我国古代在数学方面的成就.问题你能利用上述规律写出下一行的数值吗?提示根据规律下一行的数值分别是:172135352171.0120()C,C,C,,C,,C,.nknnnnnab的展开式的二项式系数有很多有趣的性质而且我们可以从不同角度进行研究n(a+b)n的展开式的二项式系数123456(),6.31.nab用计算工具计算的展开式的二项式系数并填入表11121133114641151010511615201561环节二:观察分析,感知概念11121133114641151010511615201561通过计算、填表,你发现了什么规律?从表6.3-1可以发现,每一行中的系数具有对称性.除此以外还有什么规律呢?为了便于发现规律,上表还可以写成如图6.3-1所示的形式.1()ab2()ab3()ab4()ab5()ab6()ab…………………………………………………………………………………………………………………………………………………观察图6.3-1,你还能发现哪些规律?CCCC012(),,,,,.C,{0,1,2,,}.nnnnnnrnabrn对于的展开式的二项式系数我们还可以从函数的角度分析它们可看成以为自变量的函数其定义域是环节三:抽象概括,形成概念C6,()({0,1,2,3,4,,7,6.32,5,6})rnnfrrn对于确定的我们还可以画出它的图象.例如当的图象是个时函离散点如图数所示.7个孤立的点Orf(r)6361420(1)7,8,9()C,6.32,?(2),?rnnfr探究时函数的图象观察图你发现了什么规律请你分别画出比较它们的异同你发现了什么规律7n8nf(r)n为奇数;如n=72n20103035On7432nf(r)rnO615201n为偶数;如n=61.“”,CC.mnmnn对称性与首末两端等距离的两个二项式系数相等.事实上这一性质可直接由得到2()C,.rnnrfr直线将函数的图象分成对称的两部分它是图象的对称轴环节四:辨析理解,深化概念111211331146411510105116152015611C(1()(1)11CC,.)2,(1!Ckkknnnnknnnnknknknkkkkk增减性与)因为最即大值11,1,,C;21,,C.2knknnknkkknkk...