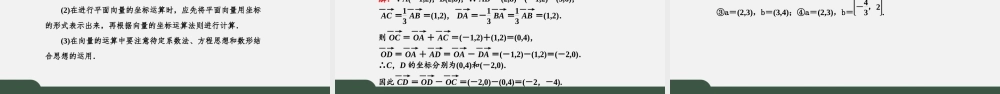6.3.2-4平面向量的正交分解、加减运算&数乘运算及坐标表示新课程标准1.借助平面直角坐标系,掌握平面向量的正交分解及坐标表示.2.会用坐标表示平面向量的加、减运算与数乘运算.新学法解读1.向量的正交分解实际上是平面向量基本定理的特例.2.向量的坐标运算是一种代数运算,其加、减及数乘的实质是同名坐标之间的运算.[思考发现]1.下列说法正确的有()①向量的坐标即此向量终点的坐标;②位置不同的向量其坐标可能相同;③一个向量的坐标等于它的终点坐标减去它的起点坐标;④相等向量的坐标一定相同.A.1个B.2个C.3个D.4个解析:向量的坐标是其终点坐标减去起点坐标,故①错误,②③④正确.故选C.答案:C2.已知MN―→=(2,3),则点N位于()A.第一象限B.第二象限C.第三象限D.不确定解析:因为点M的位置不确定,所以点N的位置也不确定.故选D.答案:D3.已知向量a=(2,4),b=(-1,1),则2a-b=()A.(5,7)B.(5,9)C.(3,7)D.(3,9)解析:因为a=(2,4),b=(-1,1),所以2a-b=(2×2-(-1),2×4-1)=(5,7).故选A.答案:A4.已知向量a=(x+3,x2-3x-4)与AB―→相等,其中A(1,2),B(3,2),则x的值为()A.-1B.-1或4C.4D.1或-4解析: AB―→=(2,0),又 a=AB―→,∴x+3=2,x2-3x-4=0,解得x=-1.故选A.答案:A5.如果向量a=(k,1),b=(4,k)共线且方向相反,则k等于()A.±2B.2C.-2D.0解析:由a,b共线得k2=4,所以k=±2,又两个向量的方向相反,故k=-2.故选C.答案:C[系统归纳]1.关于平面向量的坐标表示(1)向量的坐标只与向量的起点、终点有关,而与向量的具体位置无关.(2)当向量确定以后,向量的坐标就是唯一确定的,因此向量在平移前后,其坐标不变.2.点的坐标与向量的坐标(1)区别:(ⅰ)表达形式:向量a=(x,y),点A(x,y);(ⅱ)意义不同:点A(x,y)表示点A在平面直角坐标系中的位置;向量a=(x,y)表示向量的大小、方向.(2)联系:当平面向量的起点在原点时,向量的坐标与终点的坐标相同.3.关于平面向量的坐标运算(1)平面向量的加、减、数乘运算结果仍然是向量,坐标运算的结果仍然是坐标.(2)进行向量的坐标运算时,要结合向量运算的三角形法则和平行四边形法则,先化简向量,再进行坐标运算.4.要正确理解向量平行的条件(1)a∥b(b≠0)⇔a=λb.这是几何运算,体现了向量a与b的长度及方向之间的关系.(2)a∥b⇔x1y2-x2y1=0,其中a=(x1,y1),b=(x2,y2).这是代数运算,由于不需...