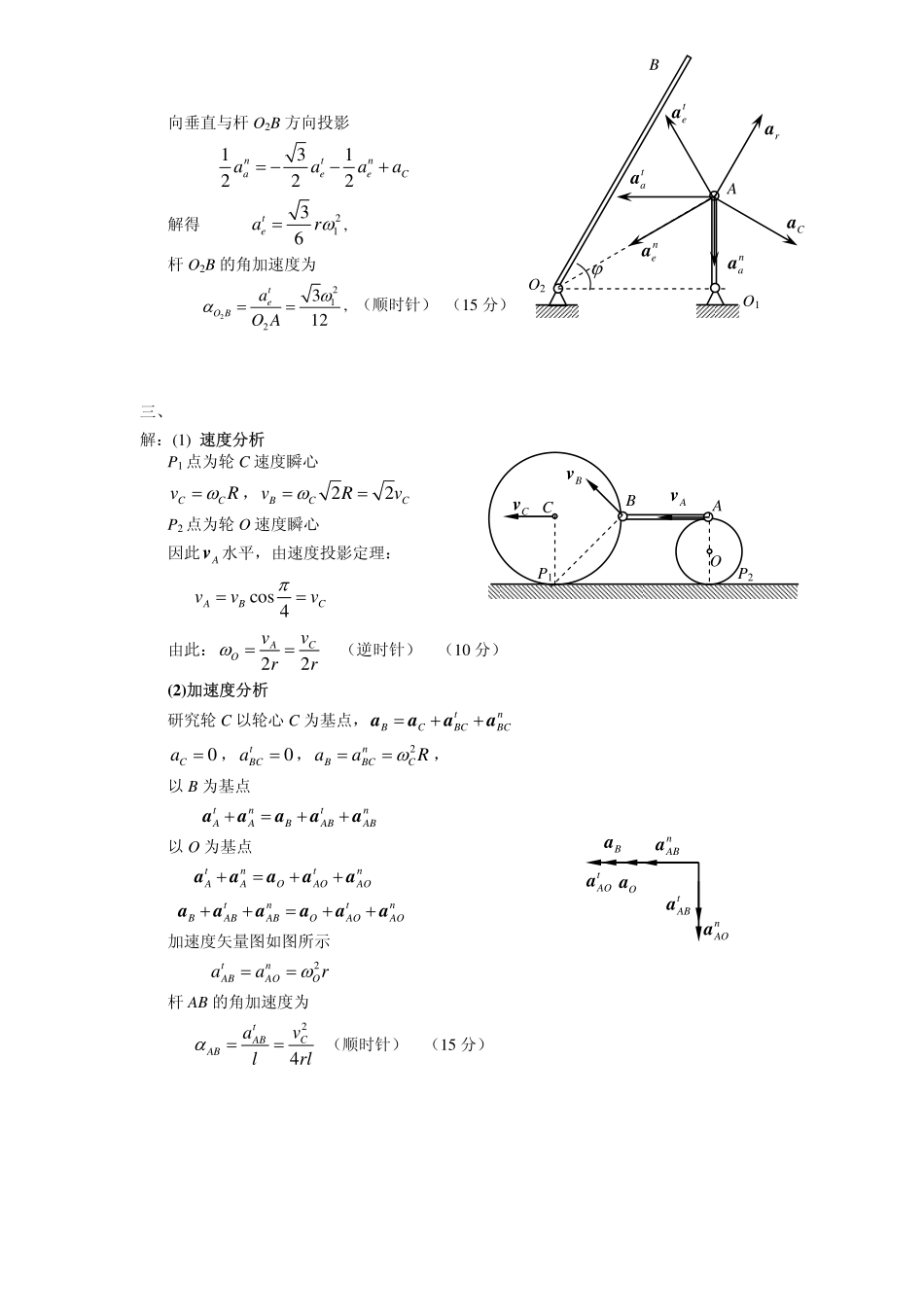
随堂测试-3一、解:取整体,受力如图。∑=0)(FAM0BFaM⋅−=得:/BFMa=∑=0xF0=+BAxFF得:/AxFMa=−∑=0yF0AyF=DE杆为二力杆,取ACE,受力如图。∑=0)(FCM220AxDEFaFa⋅+⋅=得:2/DEFMa=∑=0xF022=−+DECxAxFFF得:2/CxFMa=∑=0yF022=−+DECyAyFFF得:/CyFMa=二、解:选A为动点,杆O2B为动系,aer=+vvv速度平行四边形如图所示sin()sinsinaervvvπϕθϕθ==−−则1eravvvrω===21222eeOBvvOArωω===(逆时针)(10分)tntnaaeerC+=+++aaaaaa杆O1A以匀角速转动0taa=;21naarω=;222122neOBraOAωω==2212COBravrωω==ABCDEaaaaaaMACEFAxFAyFCxFCyFDEO2ϕO1avevrvBAθ向垂直与杆O2B方向投影131222ntnaeeCaaaa=−−+解得2136tearω=,杆O2B的角加速度为2212312teOBaOAωα==,(顺时针)(15分)三、解:(1)速度分析P1点为轮C速度瞬心CCvRω=,22BCCvRvω==P2点为轮O速度瞬心因此Av水平,由速度投影定理:cos4ABCvvvπ==由此:22CAOvvrrω==(逆时针)(10分)(2)加速度分析研究轮C以轮心C为基点,tnBCBCBC=++aaaa0Ca=,0tBCa=,2nBBCCaaRω==,以B为基点tntnAABABAB+=++aaaaa以O为基点tntnAAOAOAO+=++aaaaatntnBABABOAOAO++=++aaaaaa加速度矢量图如图所示2tnABAOOaarω==杆AB的角加速度为24tCABABvalrlα==(顺时针)(15分)BatABanABanAOaOatAOaBACOCvBvP1P2AvO2CaϕBAO1naataateaneara