第3章4(1).pptVIP免费

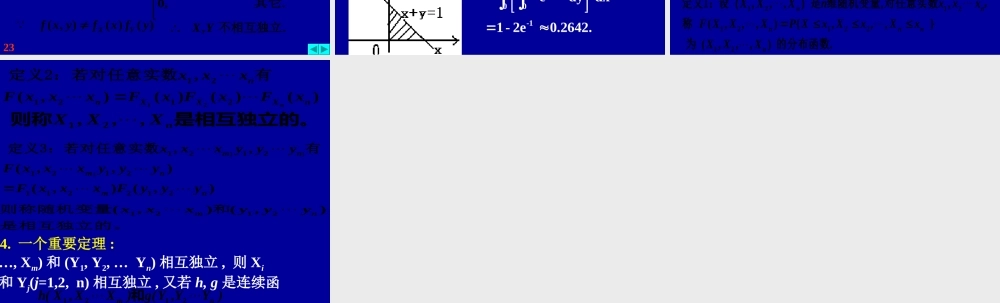
§4相互独立的随机变量独立的概念随机变量相互互独立的概念引出两个我们将利用两个事件相有若对任意及边缘分布函数的分布函数分别是、和定义：设yxYXyFxFyxFYX,,),()()(),(.1},{}{},{yYPxXPyYxXP即)()(),(yFxFyxFYX.是相互独立的和则称YX几乎处处成立相互独立和)()(),(yfxfyxfYXYX密度，则的概率密度和边缘概率分别是、和是连续型随机变量，设定理：)Y,X()y(f)x(f)y,x(f)Y,X().(.YX12这里“几乎处处成立”的含义是：在平面上除去面积为0的集合外，处处成立.P(AB)=P(A)P(B)yyjxxiYXyyijxxYXjijiPP)y(F)x(FP)y,x(F)y(F)x(F)y,x(F证：yyjixxyyjxxiyyijxxjijijiPPPPPjiijPPP则是离散型型随机变量，设),().2(YX,2,1,jipppYXjiij相互独立和XY41811234432112116181121161161161121000000ip411p412p413p414pjp48132p48251p4873p4834p21故X,Y不独立。:),(:的分布律为设例题YX是否独立？问：YX,,2,1,jipppYXjiij相互独立和22dy)y,x(f)x(fX解：的概率密度为设例题),(:YX是否独立？问：YX,.,,x,dyxy其它02023102.,0,20,2其它xx.,,y,ydxxydx)y,x(f)y(fY其它0103232220)()(),(yfxfyxfYX.,相互独立YX其它,0,10,20,23),(2yxxyyxf2yx1课堂练习：备课本52xy0123的概率密度为设例题),(:YX其它,0,,10,1),(xyxyxf是否独立？问：YX,dyyxfxfX),()(解：.,0,10,1其它xdyxx.,,x,x其它0102.,0,10,11,01,11),()(11其它yyYyydxyydxdxyxfyf)()(),(yfxfyxfYX.,不相互独立YX例:设X和Y都服从参数=1的指数分布且相互独立试求P{X+Y≤1}.XY-x-yXY:f(x)f(y)XY,e,x0,e,y0,f(x)f(y)0,x0,0,y0,解设和分别为和的密度函数则XYxy1XY,f(x,y)f(x)f(y).P{XY1}f(x,y)dxdy由于与相互独立故其联合密度函数为故11x-(xy)00-1edydx1-2e0.2642..,y,x,e)y,x(f)yx(其它000，若),,,,(~),(222121NYX),(~),,(~222211NYNX则.0)()(),(yfxfyxfYX.0相互独立和YX),(YX对二维正态分布)PP(.n9493...