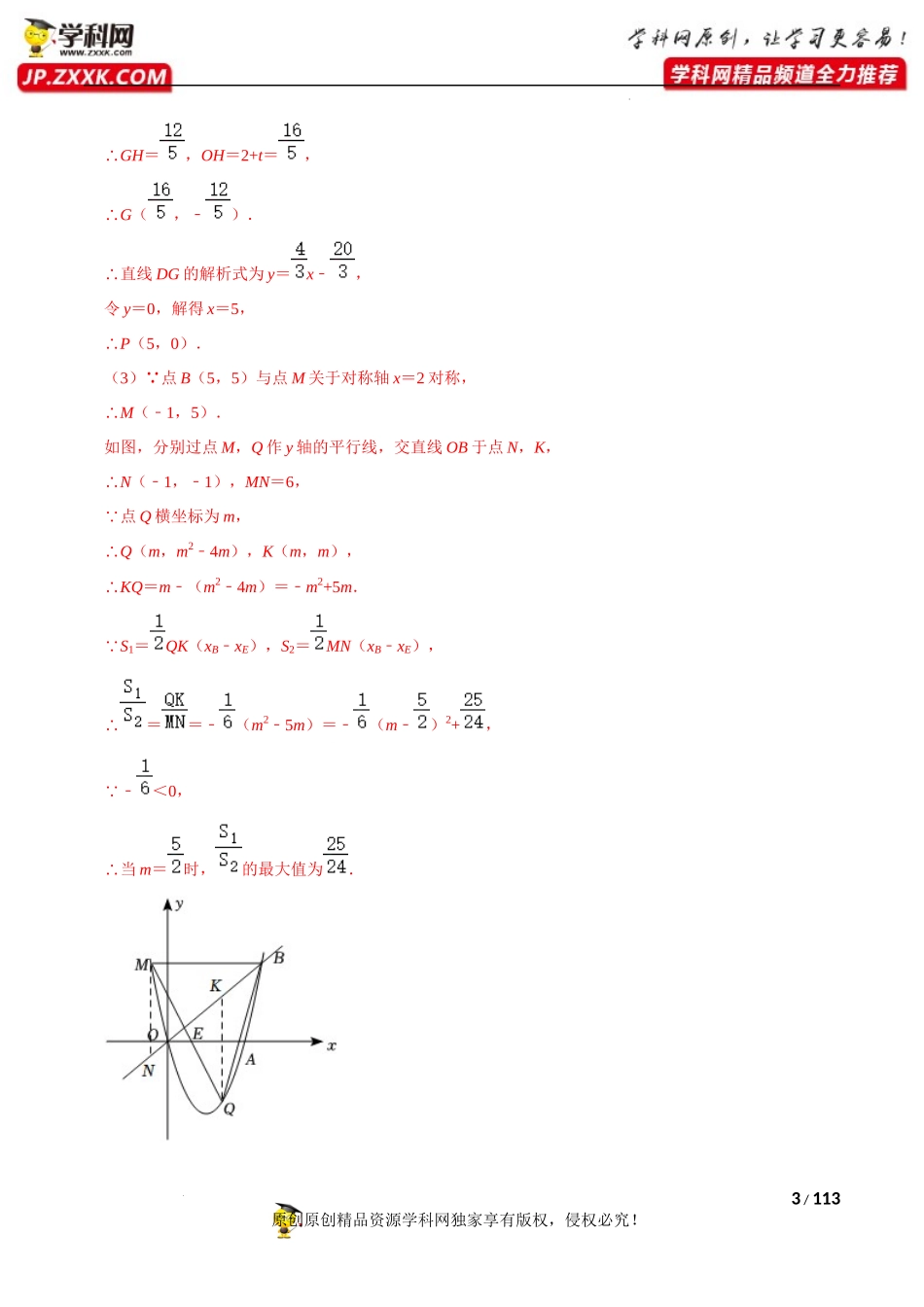
1/113原创原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司备战2023年中考数学必刷真题考点分类专练(全国通用)专题13二次函数综合问题一.解答题(共40小题)1.(2022•孝感)抛物线y=x24﹣x与直线y=x交于原点O和点B,与x轴交于另一点A,顶点为D.(1)直接写出点B和点D的坐标;(2)如图1,连接OD,P为x轴上的动点,当tan∠PDO=时,求点P的坐标;(3)如图2,M是点B关于抛物线对称轴的对称点,Q是抛物线上的动点,它的横坐标为m(0<m<5),连接MQ,BQ,MQ与直线OB交于点E.设△BEQ和△BEM的面积分别为S1和S2,求的最大值.【分析】(1)令y=x24﹣x=x,求出x的值即可得出点B的坐标,将函数y=x24﹣x化作顶点式可得出点D的坐标;(2)过点D作DE⊥y轴于点E,易得tan∠ODE=,作∠ODG=∠ODE,则点P为直线DG与x轴的交点;过点O作OG⊥DP于点G,过点G作x轴的垂线,交DE所在直线于点F,交x轴于点H,易证△ODE≌△ODG,△GDF∽△OGH,则DG=DE=2,OG=OE=4,DG:OG=DF:HG=GF:OH,2/113原创原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司设DF=t,则HG=2t,FG=42﹣t,OH=84﹣t,又OH=EF,则84﹣t=2+t,解得t的值可得出点G的坐标,进而可得直线DG的解析式,令y=0即可得出点P的坐标;(3)分别过点M,Q作y轴的平行线,交直线OB于点N,K,则S1=QK(xB﹣xE),S2=MN(xB﹣xE),由点Q的横坐标为m,可表达,再利用二次函数的性质可得出结论.【解析】(1)令y=x24﹣x=x,解得x=0或x=5,∴B(5,5); y=x24﹣x=(x2﹣)24﹣,∴顶点D(2,﹣4).(2)如图,过点D作DE⊥y轴于点E,∴DE=2,OE=4,tan∴∠ODE=,作∠ODG=∠ODE,则点P为直线DG与x轴的交点;过点O作OG⊥DP于点G,过点G作x轴的垂线,交DE所在直线于点F,交x轴于点H,∴△ODE≌△ODG(AAS),∴DG=DE=2,OG=OE=4, ∠OHG=∠F=90°,∠OGH+∠DGF=90°,∠OGH+∠GOH=90°,∴∠DGF=∠GOH,∴△GDF∽△OGH,∴DG:OG=DF:HG=GF:OH=1:2,设DF=t,则HG=2t,FG=42﹣t,OH=84﹣t, ∠DEO=∠F=∠OHG=90°,∴四边形OEFH是矩形,∴OH=EF,84∴﹣t=2+t,解得t=,3/113原创原创精品资源学科网独家享有版权,侵权必究!学科网(北京)股份有限公司∴GH=,OH=2+t=,∴G(,﹣).∴直线DG的解析式为y=x﹣,令y=0,解得x=5,∴P(5,0).(3) 点B(5,5)与点M关于对称轴x=2对称,∴M(﹣1,...