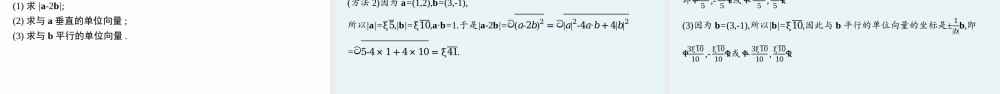高中同步学案优化设计GAOZHONGTONGBUXUEANYOUHUASHEJI1.5.2数量积的坐标表示及其计算第1章2022内容索引0102课前篇自主预习课堂篇探究学习课标阐释1.能用坐标表示平面向量数量积,会表示两个向量的模、夹角.(数学运算)2.能用坐标表示平面向量垂直的条件.(数学运算、逻辑推理)思维脉络课前篇自主预习【激趣诱思】“我知道我一直有双隐形的翅膀,带我飞,飞过绝望.不去想他们拥有美丽的太阳,我看见每天的夕阳也会有变化,我知道我一直有双隐形的翅膀,带我飞,给我希望……”如果能为平面向量的数量积插上“翅膀”,它又能飞多远呢?本节讲解平面向量数量积的“翅膀”——坐标表示,它使平面向量的数量积同时具有几何形式和代数形式的“双重身份”,从而可以使几何问题数量化,把“定性”研究推向“定量”研究.【知识点拨】知识点一:数量积的坐标表示两个向量a=(x1,y1),b=(x2,y2)的数量积的坐标表达式为a·b=(x1,y1)·(x2,y2)=x1x2+y1y2.微练习若向量a=(4,-2),b=(-1,-6),则a·b=.答案8解析a·b=4×(-1)+(-2)×(-6)=8.知识点二:计算公式1.向量的长度(1)a·a=|a|2.2.夹角余弦值根据两个非零向量a=(x1,y1),b=(x2,y2)数量积的定义,得到计算两向量夹角3.垂直条件已知向量a=(x1,y1),b=(x2,y2),则a⊥b⇔a·b=0⇔x1x2+y1y2=0.(2)若a=(x,y),则|a|=ξ𝑎·𝑎=ඥ𝑥2+𝑦2.余弦值的公式为cos
=𝑎·𝑏|𝑎||𝑏|=𝑥1𝑥2+𝑦1𝑦2ට(𝑥12+𝑦12)(𝑥22+𝑦22).要点笔记已知a=(a1,a2),b=(b1,b2),a∥b⇔a1b2-a2b1=0;a⊥b⇔a1b1+a2b2=0.这两个结论容易混淆,可分别简记为“纵横交错积的差为零,横横纵纵积的和为零”.微练习(1)设a=(-2,3),则|a|=.(2)若a=(4,-3),b=(-8,-6),则a,b夹角的余弦值等于.(3)若向量a=(3,x),b=(2,-6),且a⊥b,则x=.答案(1)ξ13(2)-725(3)1=-32+18ට42+(-3)2×ට(-8)2+(-6)2=-145×10=-725.(3)因为a⊥b,所以a·b=0,即3×2+(-6)x=0,解得x=1.解析(1)|a|=ට(-2)2+32=ξ13.(2)设a,b的夹角为θ,则cosθ=𝑎·𝑏|𝑎||𝑏|课堂篇探究学习探究一数量积的坐标运算角度1数量积的基础坐标运算例1已知向量a=(-1,2),b=(3,2).(1)求a·(a-b);(2)求(a+b)·(2a-b);(3)若c=(2,1),求(a·b)c,a(b·c).分析根据坐标运算法则,结合数量积的运算律进行计算.解(1)(方法1) a=(-1,2),b=(3,2),∴a-b=(-4,0).∴a·(a-b)=(-1,2)·(-4,0)=(-1)×(-4)+2×0=4.(方法2)a·(a-b)=a2-a·b=(-1)2+22-[(-1)×3+2×2]=4.(2) a+b=(-1,2)+(3,2)=(2,4),2a-b=2(-1,2)-(3,2)=(-2,4)-(3,2)=(-5,2),∴(a+b)·(2a-b)=(2...