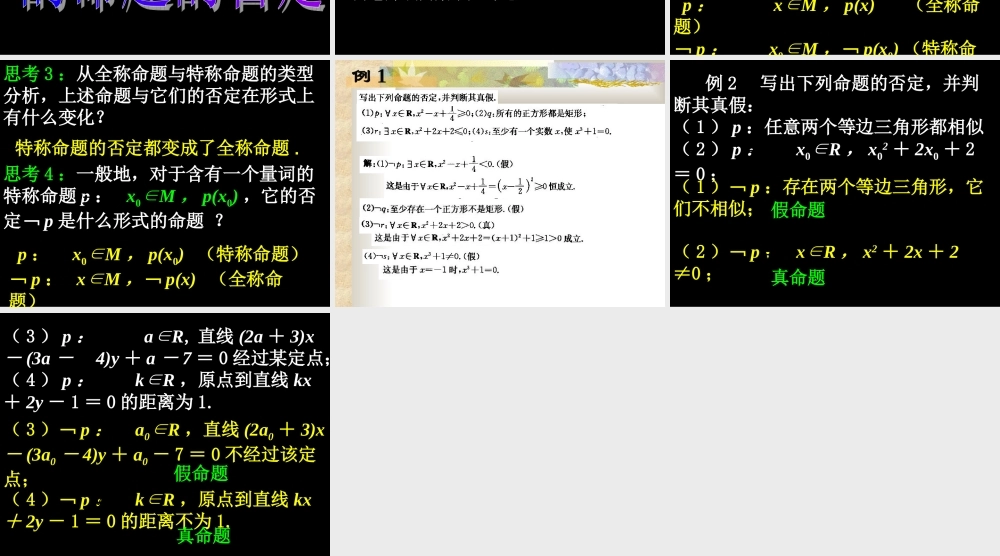
1.4全称量词与存在量词第二课时问题提出1.全称量词与存在量词的含义及其符号表示分别是什么?存在量词:表示“部分”的量词,用符号“”表示.全称量词:表示“全体”的量词,用符号“”表示;2.全称命题与特称命题的含义及其一般表示形式分别是什么?一般表示形式含义含有全称量词的命题特称命题全称命题含有存在量词的命题xM,p(x)∈x0M,p(x∈0)3.如何判断全称命题与特称命题的真假?"假命题真命题对任意xM∈都有p(x)成立存在x0M∈使得p(x0)成立x0M,∈p(x0)xM,∈p(x)存在x0M∈使得p(x0)不成立对任意xM∈p(x)不成立看课本P24---P25掌握全称命题和特称命题的否定形式,理解它们否定形式的关系.10分钟后回答问题(如有疑问可以问老师或同桌小声讨论)思考1:从全称命题与特称命题的类型分析,上述命题与它们的否定在形式上有什么变化?全称命题的否定都变成了特称命题.思考2:一般地,对于含有一个量词的全称命题p:xM∈,p(x),它的否定﹁p是什么形式的命题?p:xM∈,p(x)(全称命题)﹁p:x0M∈,﹁p(x0)(特称命思考3:从全称命题与特称命题的类型分析,上述命题与它们的否定在形式上有什么变化?特称命题的否定都变成了全称命题.思考4:一般地,对于含有一个量词的特称命题p:x0M∈,p(x0),它的否定﹁p是什么形式的命题?p:x0M∈,p(x0)(特称命题)﹁p:xM∈,﹁p(x)(全称命题)例1例2写出下列命题的否定,并判断其真假:(1)p:任意两个等边三角形都相似(2)p:x0R∈,x02+2x0+2=0;(1)﹁p:存在两个等边三角形,它们不相似;(2)﹁p:xR∈,x2+2x+2≠0;假命题真命题(3)p:aR∈,直线(2a+3)x-(3a-4)y+a-7=0经过某定点;(4)p:kR∈,原点到直线kx+2y-1=0的距离为1.(3)﹁p:a0R∈,直线(2a0+3)x-(3a0-4)y+a0-7=0不经过该定点;假命题(4)﹁p:kR∈,原点到直线kx+2y-1=0的距离不为1.真命题