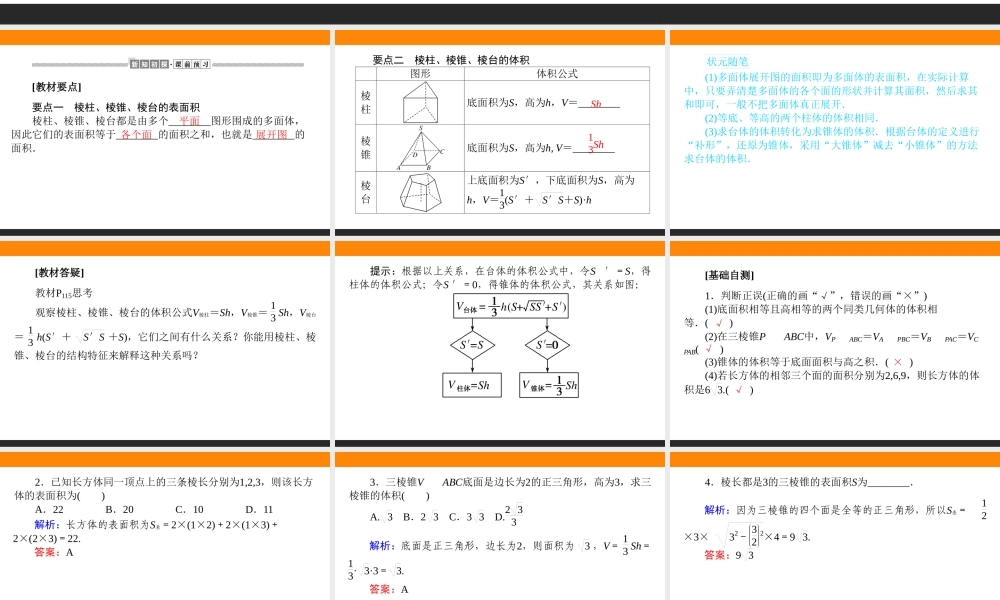
8.3.1棱柱、棱锥、棱台的表面积和体积[教材要点]要点一棱柱、棱锥、棱台的表面积棱柱、棱锥、棱台都是由多个________图形围成的多面体,因此它们的表面积等于________的面积之和,也就是________的面积.平面各个面展开图要点二棱柱、棱锥、棱台的体积图形体积公式棱柱底面积为S,高为h,V=________棱锥底面积为S,高为h,V=________棱台上底面积为S′,下底面积为S,高为h,V=13(S′+S′S+S)·hSh13Sh状元随笔(1)多面体展开图的面积即为多面体的表面积,在实际计算中,只要弄清楚多面体的各个面的形状并计算其面积,然后求其和即可,一般不把多面体真正展开.(2)等底、等高的两个柱体的体积相同.(3)求台体的体积转化为求锥体的体积.根据台体的定义进行“补形”,还原为锥体,采用“大锥体”减去“小锥体”的方法求台体的体积.[教材答疑]教材P115思考观察棱柱、棱锥、棱台的体积公式V棱柱=Sh,V棱锥=13Sh,V棱台=13h(S′+S′S+S),它们之间有什么关系?你能用棱柱、棱锥、棱台的结构特征来解释这种关系吗?提示:根据以上关系,在台体的体积公式中,令S′=S,得柱体的体积公式;令S′=0,得锥体的体积公式,其关系如图:[基础自测]1.判断正误(正确的画“√”,错误的画“×”)(1)底面积相等且高相等的两个同类几何体的体积相等.()(2)在三棱锥PABC中,VPABC=VAPBC=VBPAC=VCPAB()(3)锥体的体积等于底面面积与高之积.()(4)若长方体的相邻三个面的面积分别为2,6,9,则长方体的体积是63.()√√×√2.已知长方体同一顶点上的三条棱长分别为1,2,3,则该长方体的表面积为()A.22B.20C.10D.11解析:长方体的表面积为S表=2×(1×2)+2×(1×3)+2×(2×3)=22.答案:A3.三棱锥VABC底面是边长为2的正三角形,高为3,求三棱锥的体积()A.3B.23C.33D.233解析:底面是正三角形,边长为2,则面积为3,V=13Sh=13·3·3=3.答案:A4.棱长都是3的三棱锥的表面积S为________.解析:因为三棱锥的四个面是全等的正三角形,所以S表=12×3×32-322×4=93.答案:93题型一棱柱、棱锥、棱台的表面积——自主完成1.过长方体一个顶点的三条棱长的比是1:2:3,体对角线的长是214,则这个长方体的表面积为()A.40B.44C.72D.88解析:设过长方体一个顶点的三条棱长分别为x,2x,3x,由已知得x2+(2x)2+(3x)2=(214)2解得x=2所以三条棱长分别2,4,6.所以长方体的表面积为S=2(2×4+2×6+4×6)=88.答案:D2.所有棱长均为2的正三...