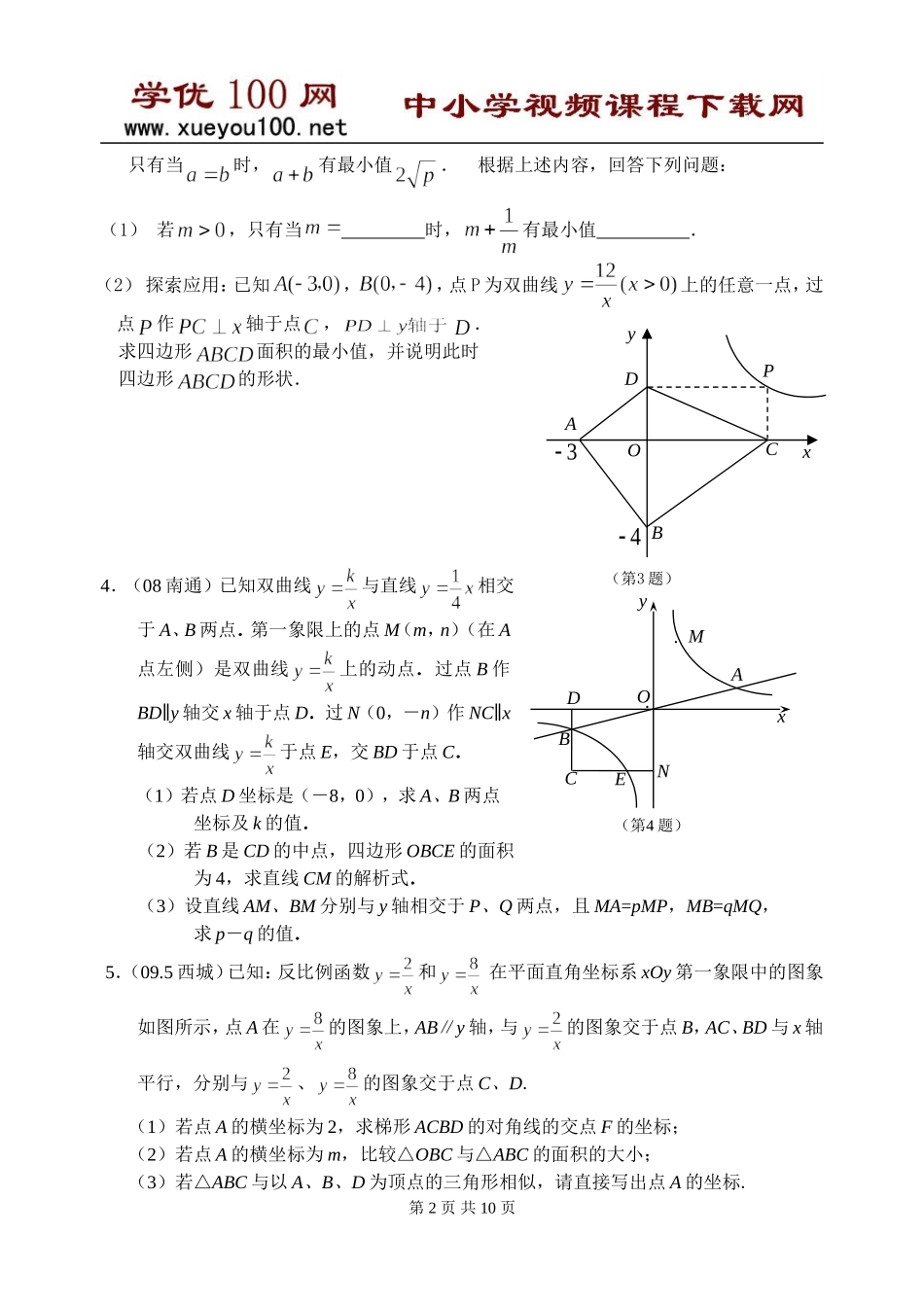
代数与几何综合题代数与几何综合题从内容上来说,是把代数中的数与式、方程与不等式、函数,几何中的三角形、四边形、圆等图形的性质,以及解直角三角形的方法、图形的变换、相似等内容有机地结合在一起,同时也融入了开放性、探究性等问题,如探究条件、探究结论、探究存在性等。经常考察的题目类型主要有坐标系中的几何问题(简称坐标几何问题),以及图形运动过程中求函数解析式问题等。解决代数与几何综合题,第一,需要认真审题,分析、挖掘题目的隐含条件,翻译并转化为显性条件;第二,要善于将复杂问题分解为基本问题,逐个击破;第三,要善于联想和转化,将以上得到的显性条件进行恰当地组合,进一步得到新的结论,尤其要注意的是,恰当地使用分析综合法及方程与函数的思想、转化思想、数行结合思想、分类与整合思想等数学思想方法,能更有效地解决问题。第一类:与反比例函数相关1.(09北京)如图,点C为⊙O直径AB上一点,过点C的直线交⊙O于点D、E两点,且∠ACD=45°,于点F,于点G.当点C在AB上运动时,设,,下列图象中,能表示与的函数关系的图象大致是()2.如图,在平面直角坐标系中,二次函数的图象经过正方形ABOC的三个顶点A、B、C,则m的值为.3.(09延庆)阅读理解:对于任意正实数,,,,只有当时,等号成立.结论:在(均为正实数)中,若为定值,则,第1页共10页ABCD只有当时,有最小值.根据上述内容,回答下列问题:(1)若,只有当时,有最小值.(2)探索应用:已知,,点P为双曲线上的任意一点,过点作轴于点,.求四边形面积的最小值,并说明此时四边形的形状.4.(08南通)已知双曲线与直线相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线于点E,交BD于点C.(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.5.(09.5西城)已知:反比例函数和在平面直角坐标系xOy第一象限中的图象如图所示,点A在的图象上,AB∥y轴,与的图象交于点B,AC、BD与x轴平行,分别与、的图象交于点C、D.(1)若点A的横坐标为2,求梯形ACBD的对角线的交点F的坐标;(2)若点A的横坐标为m,比较△OBC与△ABC的面积的大小;(3)若△ABC与以A、B、D为顶点的三角形相似,请直接写出点A的坐标.第2页共10页y...