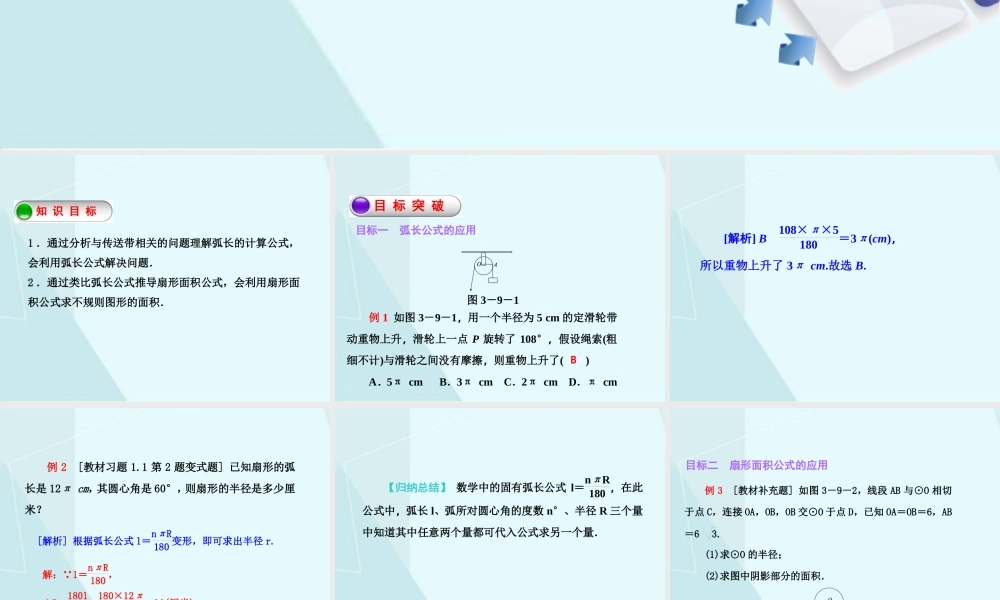
知识目标知识目标目标突破目标突破总结反思总结反思9弧长及扇形的面积知识目标1.通过分析与传送带相关的问题理解弧长的计算公式,会利用弧长公式解决问题.2.通过类比弧长公式推导扇形面积公式,会利用扇形面积公式求不规则图形的面积.目标突破目标一弧长公式的应用图3-9-1例1如图3-9-1,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了()A.5πcmB.3πcmC.2πcmD.πcmB[解析]B108×π×5180=3π(cm),所以重物上升了3πcm.故选B.例2[教材习题1.1第2题变式题]已知扇形的弧长是12πcm,其圆心角是60°,则扇形的半径是多少厘米?[解析]根据弧长公式l=nπR180变形,即可求出半径r.解: l=nπR180,∴R=180lnπ=180×12π60π=36(厘米).故扇形的半径是36厘米.【归纳总结】数学中的固有弧长公式l=nπR180,在此公式中,弧长l、弧所对圆心角的度数n°、半径R三个量中知道其中任意两个量都可代入公式求另一个量.目标二扇形面积公式的应用例3[教材补充题]如图3-9-2,线段AB与⊙O相切于点C,连接OA,OB,OB交⊙O于点D,已知OA=OB=6,AB=63.(1)求⊙O的半径;(2)求图中阴影部分的面积.图3-9-2解:(1)连接OC,则OC⊥AB. OA=OB,∴AC=BC=12AB=12×63=33.在Rt△AOC中,OC=OA2-AC2=62-(33)2=3,∴⊙O的半径为3.(2) OC=12OB,∴∠B=30°,∴∠COD=60°,∴扇形OCD的面积为60·π·32360=32π,∴阴影部分的面积=SRt△OBC-S扇形OCD=12OC·CB-32π=9323[归纳总结]由扇形面积的两个计算公式可以发现,已知S扇形,l,n,R四个量中的任意两个量,均可以求出另外两个量.同学们在解题时要根据不同问题,灵活选用合适的公式进行计算.例4教材补充例题如图3-9-3,大半圆O的弦AB与小半圆O1交于E,F两点,AB=6cm,EF=2cm,且AB∥CD.求阴影部分的面积.图3-9-3[解析]将两个半圆变为同圆心的半圆.作OM⊥AB于点M,连接OB,OF,构造直角三角形,利用所构造的两个三角形有公共边OM,可找到两个半圆的半径平方差与已知条件之间的关系:OB2-OF2=OM2+32-(OM2+12)=8,阴影部分的面积是两个半圆的面积差.代入数据求解即可.解:如图,将两个半圆变为同圆心的半圆.过点O作OM⊥AB于点M,连接OB,OF,则MF=12EF=1cm,BM=12AB=3cm,S阴影=12πOB2-12πOF2=12π(OB2-OF2)=12π[(OM2+32)-(OM2+12)]=4π(cm2).[归纳总结]重新组合求不规...