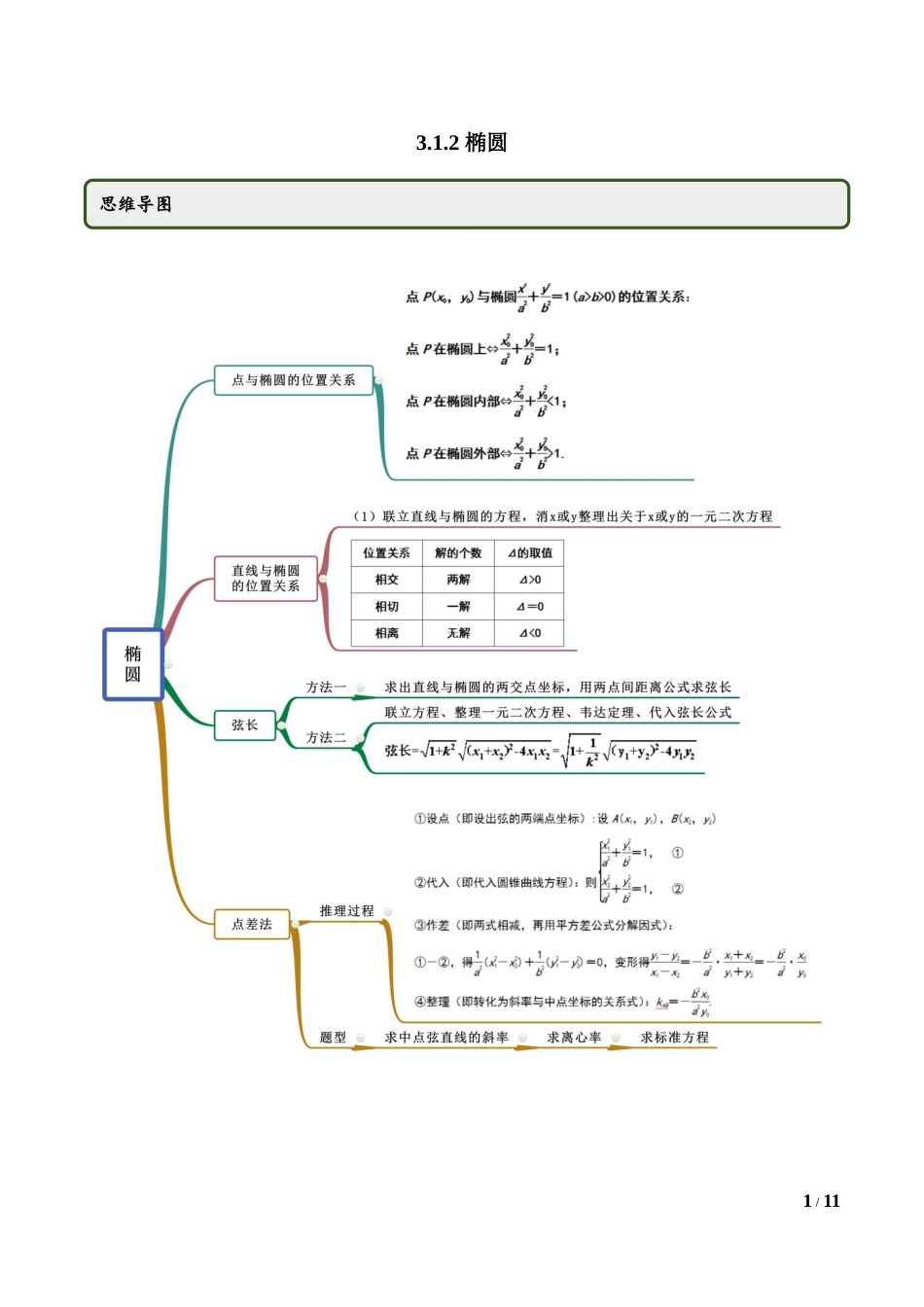
1/113.1.2椭圆思维导图2/11考点一点与椭圆的位置关系【例1】已知点P(k,1),椭圆+=1,点P在椭圆外,则实数k的取值范围为____________.【答案】∪【解析】依题意得,+>1,解得k<-或k>.【一隅三反】1.已知点(1,2)在椭圆+=1(n>m>0)上,则m+n的最小值为________.【答案】9【解析】依题意得,+=1,而m+n=(m+n)=1+++4=5++≥5+2=9,当且仅当n=2m时等号成立,故m+n的最小值为9.考点二直线与椭圆的位置关系【例2-1】(2020·上海高二课时练习)为何值时,直线和曲线有两个公共点?有一个公共点?没有公共点?【答案】见解析【解析】由,得,即常见考法3/11当,即时,直线和曲线有两个公共点;当,即时,直线和曲线有一个公共点;当,即时,直线和曲线没有公共点.【例2-2】(2020·吉林长春.高二月考)直线与椭圆的位置关系为()A.相切B.相交C.相离D.不确定【答案】B【解析】由题意,直线,可得直线恒过点,又由,所以点在椭圆的内部,所以直线与椭圆相交于不同的两点,故选B.【一隅三反】1.(2019·全国高二课时练习)直线与椭圆恒有两个公共点,则m的取值范围为()A.B.C.D.对于含有一个参数的直线方程,往往是过定点的,找到这个定点后,只需要这个定点在椭圆内或是椭圆上即可,也即是.4/11【答案】C【解析】已知直线y=kx+1与椭圆联立方程组可化为(m+5k2)x2+10kx+5-5m=0,要使得直线与椭圆恒有两个公共点,则△=100k2-4(m+5k2)(5-5m)=20[m2-(1-5k2)m]>0,m>0,m≠5.∴m>1-5k2,m>0,m≠5,又k∈R,∴m>1,且m≠5.∴m的取值范围为(1,5)∪(5,+∞)故选C2.(2020·全国高三课时练习(理))(2018·兰州一模)已知直线y=kx-k-1与曲线C:x2+2y2=m(m>0)恒有公共点,则m的取值范围是()A.[3,+∞)B.(-∞,3]C.(3,+∞)D.(-∞,3)【答案】A【解析】 直线方程为∴直线恒过定点 曲线的方程为∴曲线表示椭圆 直线与曲线:恒有公共点∴点在椭圆内或椭圆上,即.∴故选A.3.直线y=x+m与椭圆有两个不同的交点,则m的范围是()A.-5<m<5B.m<-,或m>C.m<D.-<m<【答案】D5/11【解析】由,得5x2+8mx+4m24=0﹣,结合题意△=64m220﹣(4m24﹣)>0,解得:-<m<,故选:D.考点三弦长【例3】(2020·云南省泸西县第一中学高二期中(文))已知椭圆x24+y29=1及直线l:y=32x+m(1)当直线l与该椭圆有公共点时,求实数m的取值范围;(2)当m=3时,求直线l被椭圆截得的弦长【答案】(1)[−3√2,...