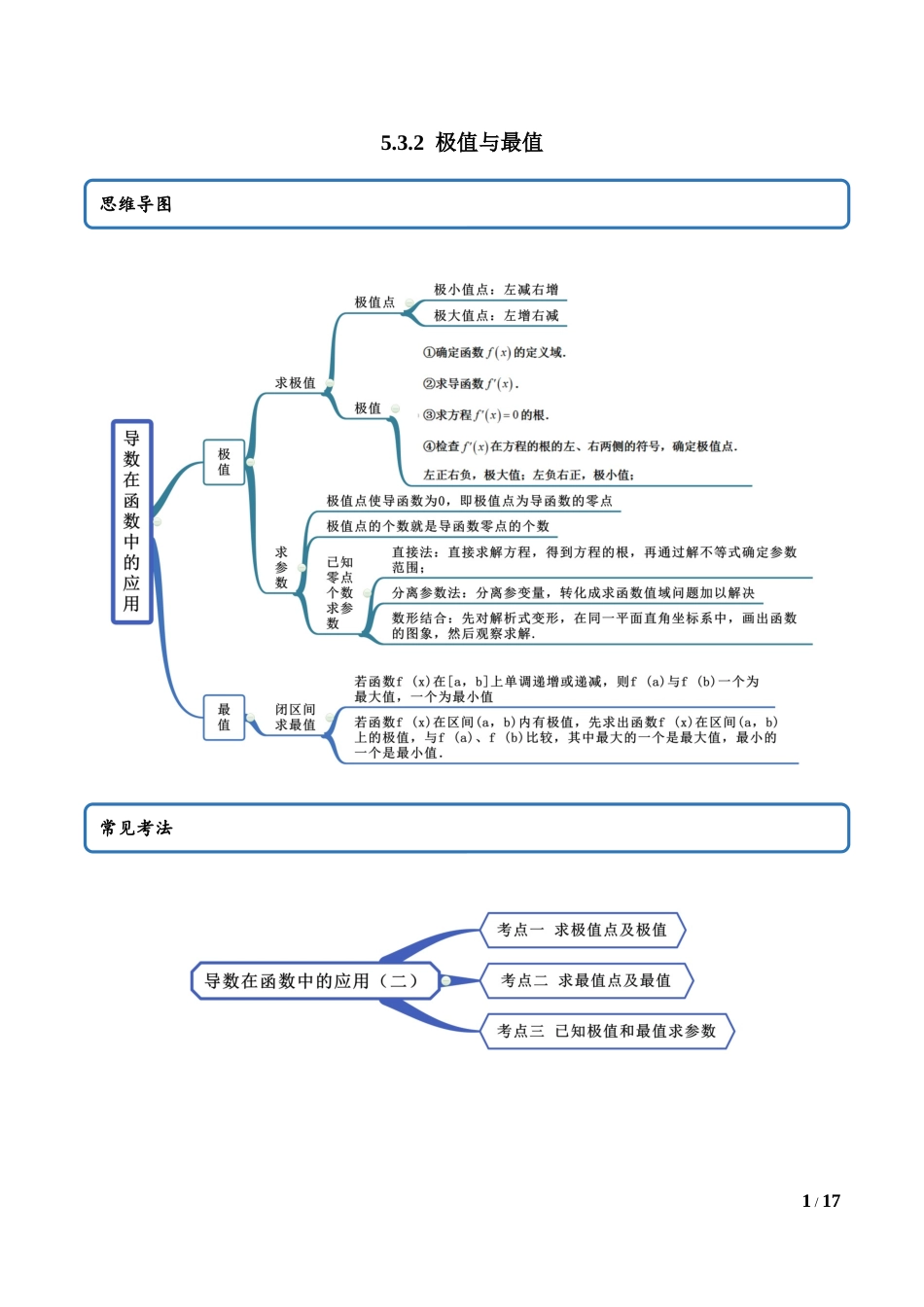
1/175.3.2极值与最值思维导图常见考法2/17考点一求极值及极值点【例3】(2020·安徽滁州·高二期末(理))已知函数在点处的切线方程为.(1)求函数的解析式;(2)求函数的单调区间和极值.【答案】(1);(2)见解析.【解析】(1),切线为,即斜率,纵坐标即,,解得,解析式(2),定义域为得到在单增,在单减,在单增极大值,极小值.【一隅三反】1.(2020·重庆高二期末)函数的极小值点为___________.【答案】2【解析】因为,所以,令,得,所以当时,,在上单调递增;3/17当时,,在上单调递减;当时,,在上单调递增;所以在时取得极小值,故填:2.2.(2020·广东云浮·高二期末)函数的极大值为__________.【答案】【解析】依题意得.所以当时,;当时,.所以,函数的单调递增区间为,单调递减区间为.所以当时,函数有极大值.故答案为:.3.(2020·四川内江·高二期末(文))已知函数.(1)求的单调区间和极值;(2)若直线是函数图象的一条切线,求的值.【答案】(1)单调递增区间为和,单调递减区间为,极大值为,极小值为;4/17(2)或.【解析】(1),定义域为,.令,解得或;令,解得.所以,函数的单调递增区间为和,单调递减区间为,函数的极大值为,极小值为;(2)令,解得或,,,所以,切点坐标为或,则有或,解得或.考点二求最值点最值【例2】.(2020·兴仁市凤凰中学高二月考(文))已知函数f(x)=x2(x-1).(1)求函数f(x)的单调区间;(2)求f(x)在区间[-1,2]上的最大值和最小值.【答案】(1)的递增区间为,递减区间为.(2)最大值,最小值.【解析】(1) ,∴.由,解得或;5/17由,解得,所以的递增区间为,递减区间为.(2)由(1)知是的极大值点,是的极小值点,所以极大值,极小值,又,,所以最大值,最小值.【一隅三反】1.(2020·四川射洪中学高二期中(文))已知函数,曲线在点处的切线方程为.(1)求的值;(2)求在上的最大值.【答案】(1),;(2)13【解析】(1)依题意可知点为切点,代入切线方程可得,,所以,即,又由,则,而由切线的斜率可知,∴,即,6/17由,解得,∴,.(2)由(1)知,则,令,得或,当变化时,,的变化情况如下表:-3-21+0-0+8↗极大值↘极小值↗4∴的极大值为,极小值为,又,,所以函数在上的最大值为13.2.(2020·霍邱县第二中学高二月考(文))已知函数().(1)若,求在上的最小值和最大值;(2)若在上是增函数,求实数的取值范围.【答案】(1)最...