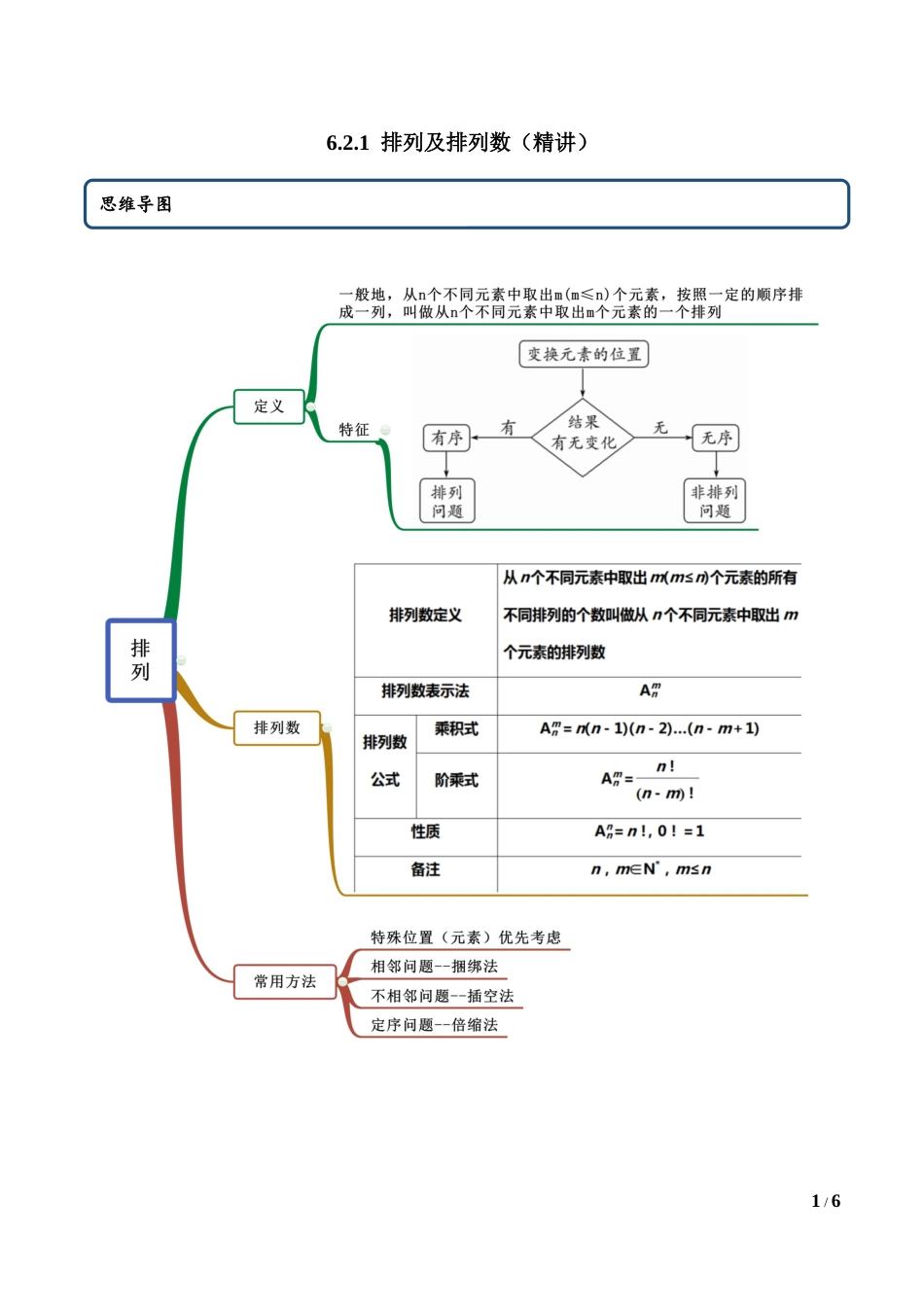
1/66.2.1排列及排列数(精讲)思维导图2/6考点一排列的概念【例1】(2021年广东汕头)(1)下列问题是排列问题的是()A.从10名同学中选取2名去参加知识竞赛,共有多少种不同的选取方法?B.10个人互相通信一次,共写了多少封信?C.平面上有5个点,任意三点不共线,这5个点最多可确定多少条直线?D.从1,2,3,4四个数字中,任选两个相加,其结果共有多少种?(2)从3个不同的数字中取出2个:①相加;②相减;③相乘;④相除;⑤一个为被开方数,一个为根指数.则上述问题为排列问题的个数为()A.2B.3C.4D.5【一隅三反】1.(2020年广东河源)判断下列问题是否为排列问题.(1)会场有50个座位,要求选出3个座位有多少种方法?若选出3个座位安排三位客人,又有多少种方法?(2)从集合M={1,2,…,9}中,任取两个元素作为a,b,可以得到多少个焦点在x轴上的椭圆方程+=1?可以得到多少个焦点在x轴上的双曲线方程-=1?(3)从1,3,5,7,9中任取3个数字,有多少种方法?若这3个数字组成没有重复的三位数,又有多少种方法?2.(2021年河北)下列问题是排列问题的是()A.从8名同学中选取2名去参加知识竞赛,共有多少种不同的选取方法?B.10个人互相通信一次,共写了多少封信?C.平面上有5个点,任意三点不共线,这5个点最多可确定多少条直线?常见考法3/6D.从1,2,3,4四个数字中,任选两个相乘,其结果共有多少种?考点二排列数【例2】(1)(2020·江苏省前黄高级中学)若,则()A.5B.6C.7D.8(2)(2020·永昌县第四中学)若,则m的值为()A.5B.3C.6D.7(3)(2021·山西省长治市第二中学校高)不等式的解集为()A.B.C.D.【一隅三反】1.(2020·全国高二单元测试)对于满足的正整数n,()A.B.C.D.2.(2020·宁夏育才中学)已知,则()A.5B.7C.10D.143.(2020·山东莱州一中)给出下列四个关系式:【方法总结】1.要注意中隐含了3个条件:①,;②;③的运算结果为正整数2.形,(即),的应用.4/6①②③④其中正确的个数为()A.1个B.2个C.3个D.4个4.(1)解不等式;(2)证明:.考点三排队问题【例3】(2021·全国高二练习)有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.(1)选5人排成一排;(2)排成前后两排,前排3人,后排4人;(3)全体排成一排,女生必须站在一起;(4)全体排成一排,男生互不相邻;(5)全体排成一排,其中甲不站最左边,也不站最右边;(6)全体排成一排,其中甲不站最左边,乙不站最右边....