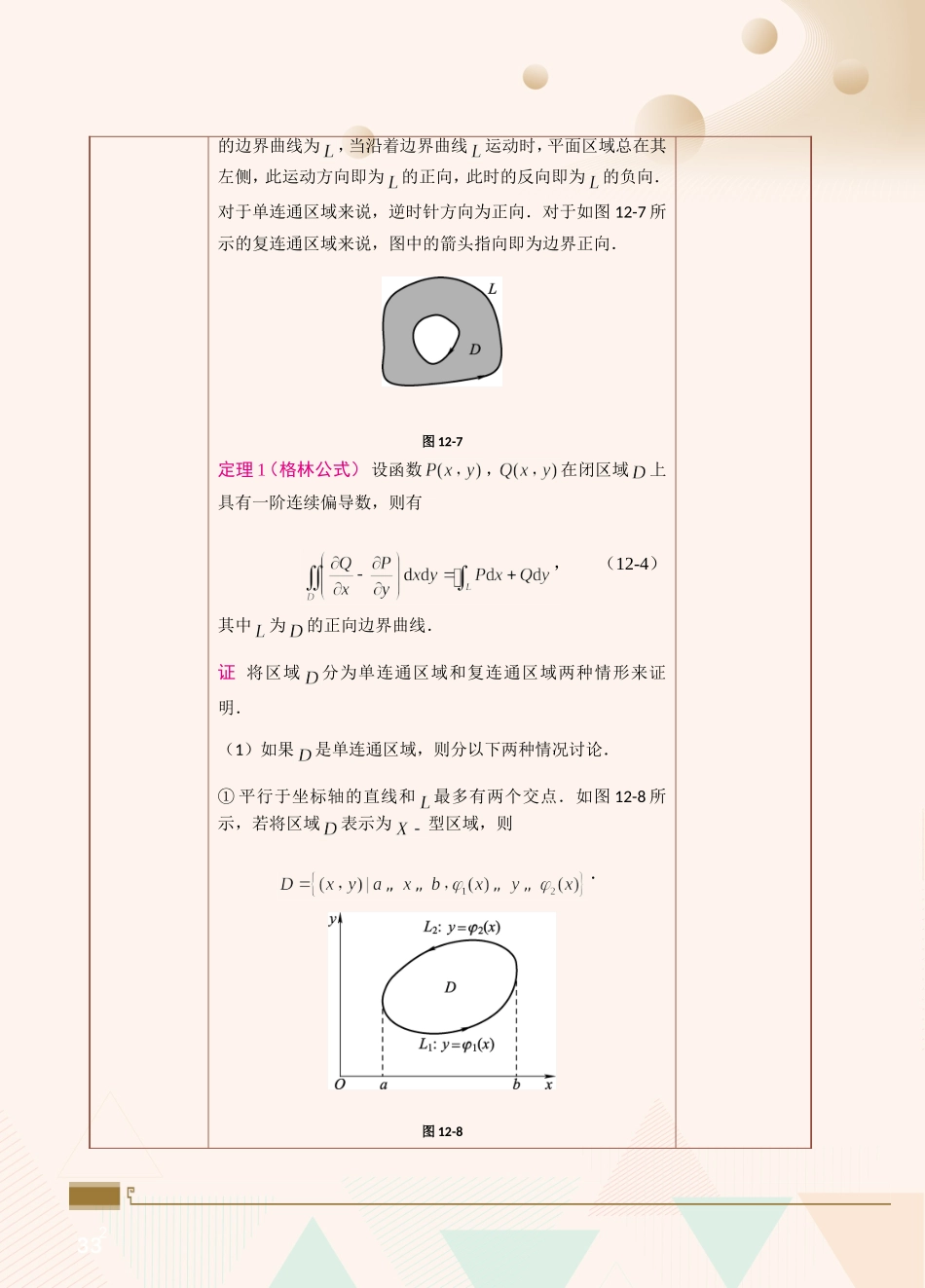
24格林公式及其应用第课课题格林公式及其应用课时2课时(90min)教学目标知识技能目标:(1)理解格林公式是联系曲线积分与二重积分的桥梁(2)掌握格林公式的应用(3)理解平面上曲线积分与路径无关的等价条件思政育人目标:通过讲解格林公式及其应用,培养学生的逻辑思维、辩证思维和创新思维能力;引导学生养成独立思考和深度思考的良好习惯;树立学生实事求是、一丝不苟的科学精神教学重难点教学重点:格林公式及其证明教学难点:格林公式的应用教学方法讲授法、问答法、讨论法、演示法、实践法教学用具电脑、投影仪、多媒体课件、教材教学设计第1节课:考勤(2min)→知识讲解(33min)→课堂测验(10min)第2节课:知识讲解(30min)→课堂测验(10min)→课堂小结(5min)教学过程主要教学内容及步骤设计意图第一节课考勤(2min)【教师】清点上课人数,记录好考勤【学生】班干部报请假人员及原因培养学生的组织纪律性,掌握学生的出勤情况知识讲解(33min)【教师】讲解格林公式的相关定义、定理,及其应用定义设为平面区域,如果内任意一条闭曲线所围成的部分都属于,则称为平面单连通区域(即内部不含有“洞”),否则称为复连通区域.例如,区域和是单连通区域;环状区域是复连通区域.关于平面区域边界曲线的正负向规定如下:设平面区域学习格林公式。边做边讲,及时巩固练习,实现教学做一体化24第课格林公式及其应用2的边界曲线为,当沿着边界曲线运动时,平面区域总在其左侧,此运动方向即为的正向,此时的反向即为的负向.对于单连通区域来说,逆时针方向为正向.对于如图12-7所示的复连通区域来说,图中的箭头指向即为边界正向.图12-7定理1(格林公式)设函数,在闭区域上具有一阶连续偏导数,则有,(12-4)其中为的正向边界曲线.证将区域分为单连通区域和复连通区域两种情形来证明.(1)如果是单连通区域,则分以下两种情况讨论.①平行于坐标轴的直线和最多有两个交点.如图12-8所示,若将区域表示为型区域,则.图12-8格林公式及其应用第课243因为连续,所以根据二重积分的计算方法有根据对坐标的曲线积分计算方法及性质,有由此可得.(12-5)若将区域表示为型区域,同理可得.(12-6)由于式(12-5)和式(12-6)同时成立,两式相加即得式(12-4).②平行于坐标轴的直线和曲线有两个以上的交点.对于这种情况,可引入辅助曲线,把区域分成有限个小区域,使每个小区域都满足①的条件.例如,如图12-9所示,对于闭...