【数三 线代第2章矩阵】考研数学历年真题（87-96）课堂笔记.pdfVIP免费

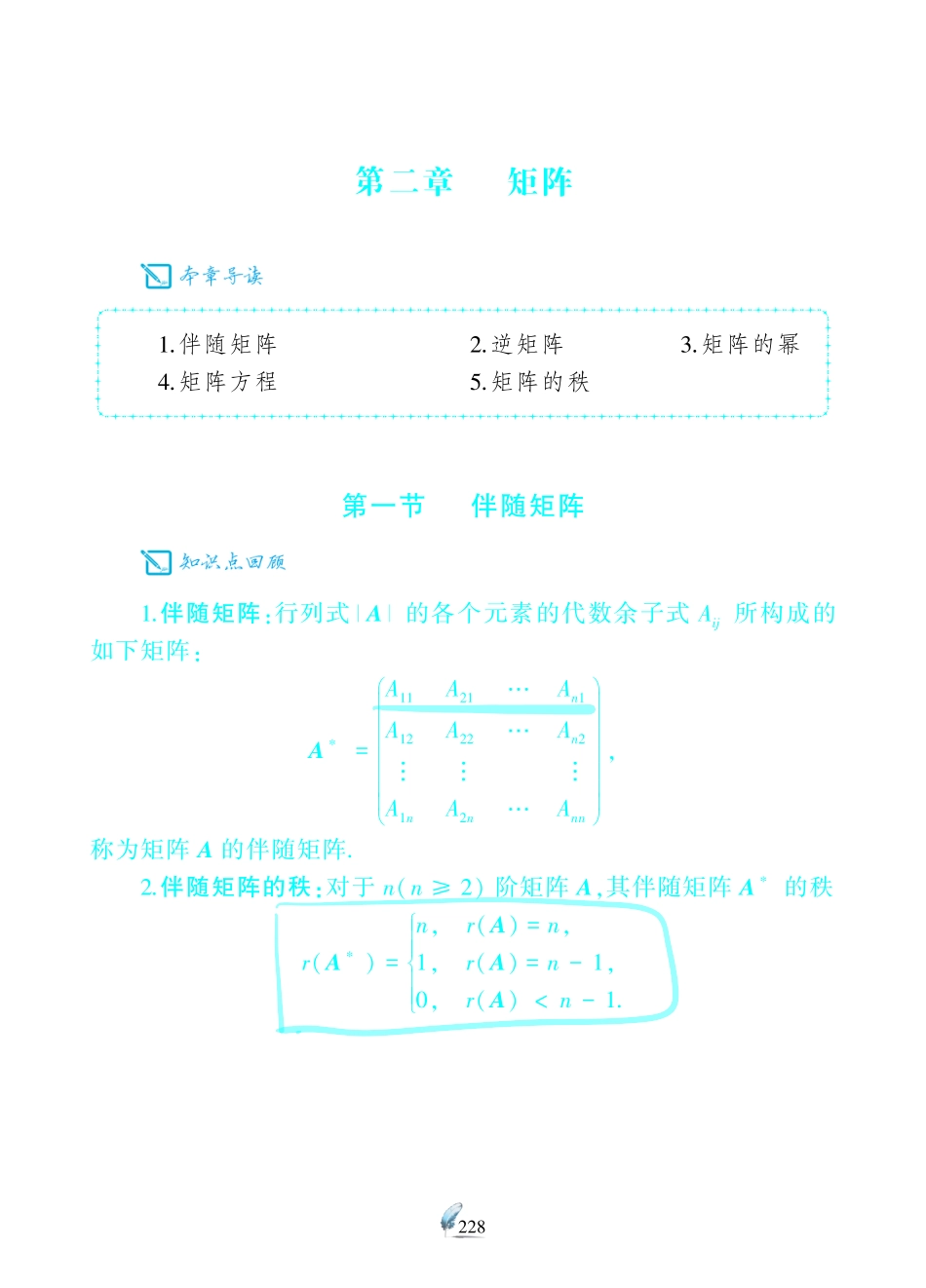
２２８第二章矩阵􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀤂􀦂􀦂􀦂􀦂１．伴随矩阵２．逆矩阵３．矩阵的幂４．矩阵方程５．矩阵的秩第一节伴随矩阵１．伴随矩阵：行列式Ａ的各个元素的代数余子式Ａｉｊ所构成的如下矩阵：Ａ∗＝Ａ１１Ａ２１…Ａｎ１Ａ１２Ａ２２…Ａｎ２︙︙︙Ａ１ｎＡ２ｎ…Ａｎｎæèçççççççöø÷÷÷÷÷÷÷，称为矩阵Ａ的伴随矩阵．２．伴随矩阵的秩：对于ｎ（ｎ≥２）阶矩阵Ａ，其伴随矩阵Ａ∗的秩ｒ（Ａ∗）＝ｎ，ｒ（Ａ）＝ｎ，１，ｒ（Ａ）＝ｎ－１，０，ｒ（Ａ）＜ｎ－１．ìîíïïïïïï２２９１（１９９０年卷Ⅴ试题）设Ａ为ｎ阶可逆矩阵，Ａ∗是Ａ的伴随矩阵，则（）（Ａ）Ａ∗＝Ａｎ－１．（Ｂ）Ａ∗＝Ａ．（Ｃ）Ａ∗＝Ａｎ．（Ｄ）Ａ∗＝Ａ－１．２（１９９６年卷Ⅳ试题）设ｎ阶矩阵Ａ非奇异（ｎ≥２），Ａ∗是矩阵Ａ的伴随矩阵，则（）（Ａ）（Ａ∗）∗＝Ａｎ－１Ａ．（Ｂ）（Ａ∗）∗＝Ａｎ＋１Ａ．（Ｃ）（Ａ∗）∗＝Ａｎ－２Ａ．（Ｄ）（Ａ∗）∗＝Ａｎ＋２Ａ．２３０３（１９９３年卷Ⅳ试题）设４阶方阵Ａ的秩为２，则其伴随矩阵Ａ∗的秩为．４（１９９５年卷Ⅳ试题）设Ａ＝１００２２０３４５æèççççöø÷÷÷÷，Ａ∗是Ａ的伴随矩阵，则（Ａ∗）－１＝．２３１５（１９９３年卷Ⅴ试题）已知３阶矩阵Ａ的逆矩阵为Ａ－１＝１１１１２１１１３æèççççöø÷÷÷÷，试求其伴随矩阵Ａ∗的逆矩阵．２３２第二节逆矩阵若矩阵Ａ可逆，则ＡＡ－１＝Ａ－１Ａ＝Ｅ．可逆矩阵的判定设Ａ为ｎ阶矩阵，则Ａ可逆（１）等价于Ａ≠０．（２）等价于ｒ（Ａ）＝ｎ．（３）等价于Ａｘ＝０只有零解．（４）等价于Ａ的行（列）向量组线性无关．（５）等价于Ａ的特征值均非零．求逆矩阵的方法（１）利用初等变换：对（Ａ，Ｅ）作初等行变换，当Ａ变为Ｅ时，Ｅ变为Ａ－１，即（Ｅ，Ａ－１）．初等变换法是适用范围最广的求逆矩阵的方法．（２）利用逆矩阵与伴随矩阵的关系先计算伴随矩阵Ａ∗和Ａ，再利用Ａ－１＝Ａ∗Ａ得到Ａ－１．方法（２）仅适用于阶数较低的矩阵．（３）公式法．分块矩阵的求逆公式：对任意ｍ阶可逆矩阵Ｐ，ｎ阶可逆矩阵Ｑ，有ＰＯＯＱæèççöø÷÷－１＝Ｐ－１ＯＯＱ－１æèçççöø÷÷÷，ＯＰＱＯæèççöø÷÷－１＝...