第八章_量子力学.pptVIP免费

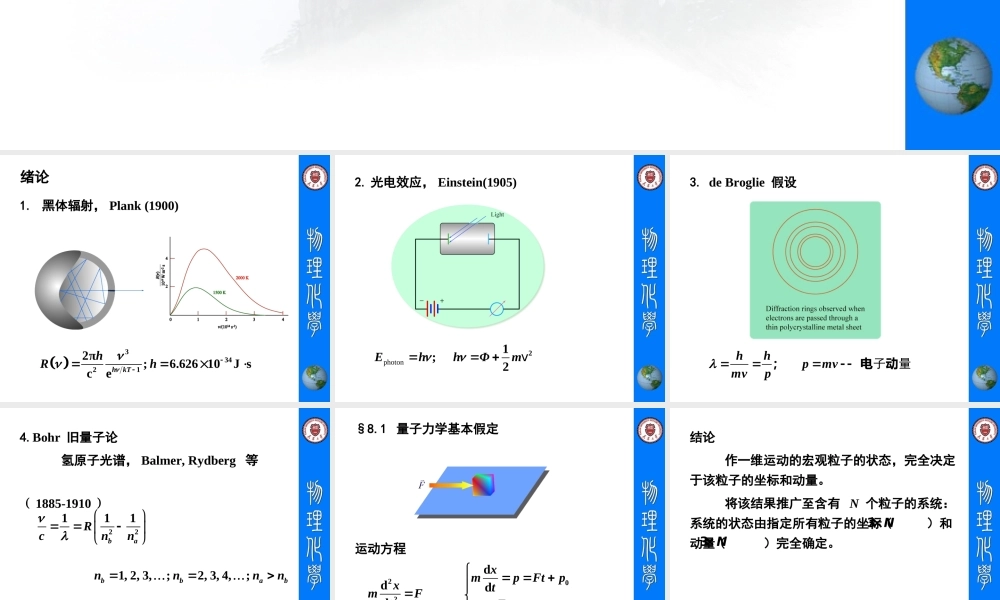
第八章量子力学基础绪论1.黑体辐射，Plank(1900)334212π;6.62610JscehkThRh2.光电效应，Einstein(1905)photon21;2EhhΦmv3.deBroglie假设hhpmvmvp；电动子量4.Bohr旧量子论氢原子光谱，Balmer,Rydberg等（1885-1910）221111,2,3,;2,3,4,;babbabRcnnnnnn§8.1量子力学基本假定运动方程22ddxmFt0200dd2xmpFtptpFxttxmm结论作一维运动的宏观粒子的状态，完全决定于该粒子的坐标和动量。将该结果推广至含有N个粒子的系统：系统的状态由指定所有粒子的坐标(）和动量(）完全确定。3×N3×N微观粒子：测不准原理推论：微观粒子的状态不能通过同时指定其坐标和动量来确定。2xxp假定一假定一包含N个粒子的微观系统，其状态由所有粒子的坐标(或动量)的函数（或)来表示，称为波函数。波函数本身没有明确的物理意义，但12(,,,)Ψtqq12(,,,)Ψtpp12(,,,)Ψtqq*11112222211112222d(,,)d(,,)d(,,)d(,,)ΨΨxyzxyzΨxyzxyz表示在时刻t，处体积元中发现粒子1,处体积元中发现粒子2……，的概率。111,,xyz1111d,,xyz222,,xyz2222d,,xyz例如，对只含一个粒子的系统，状态为则,,,Ψtxyz2(,,,)dddΨtxyzxyz表示在时刻t，处体积元发现该粒子的概率。,,xyzddddxyz对波函数的要求1.由于在整个空间找到粒子的概率为1，因此满足该条件的波函数称为平方可积的或归一化的。注：由于(为任意实数)，和代表相同的状态。即波函数可以相差因子。21212,,,...dd...1Ψtqq12,,,tqqΨΨΨΨ*iα*iαeeαΨiαeΨiαe2.波函数为单值的。3.波函数为连续的。将满足上述三个条件的波函数称为品优函数。假定二系统状态随时间的变化由薛定谔方程确定：式中代表所有粒子的坐标。(h为普朗克常数)2222222jjjjj(,)i(,)(,)2ΨtrtVtrΨtrmxyzri1,2πh令称为哈密尔顿算符。薛定谔方程简写为2222222jjjjjˆH,2Vtrmxyz,ˆH,iΨtrΨtrt考虑势能函数与时间无关的情况，令则有：得到,ΨtrTtrd11ˆHidTtrTttrˆHd1idrErTtETt...