概率习题课三.pptVIP免费

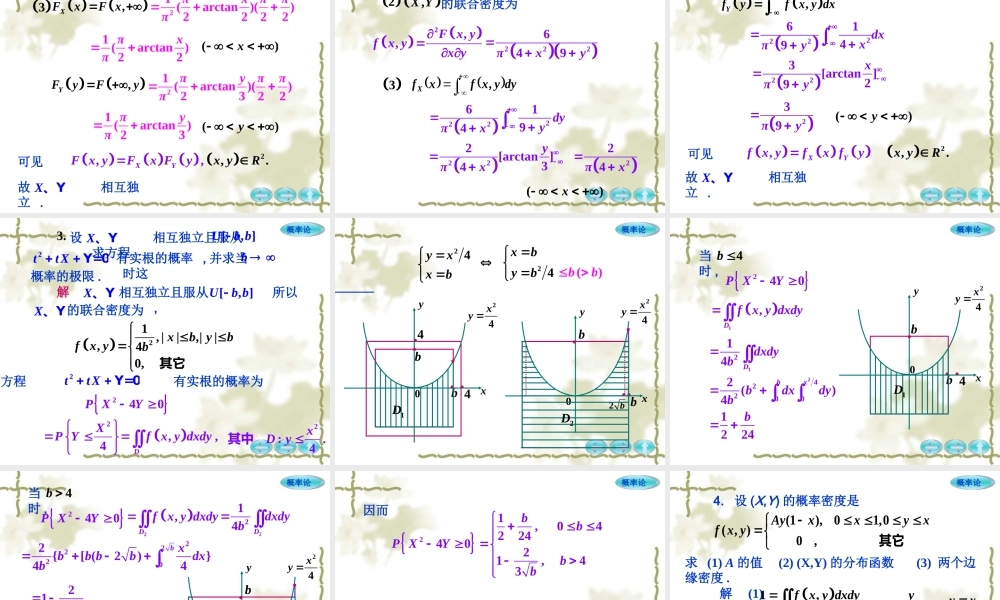
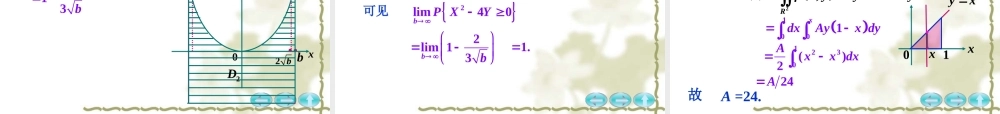概率论概率统计习题课三概率论一、填空题31.0,0,7PXY40,7PY0PXmax{,}0_____.PXY设则解max,00,0.XYXY{max,0}PXY{0,0}PXY因为所以40,7PY0PX30,7PY0PX又因为{(0)(0)}PXY10,0PXY47故334{0,0}777PXY2757概率论2.已知的分布律为XY、YX0116a13b010X1XY且与独立,则___,____.ab解{0,1}PXXY{0,1}PXYa0PX{0,0}PXY{0,1}PXY13a{1}PXY{0,1}PXY{1,0}PXYab1316概率论0X1XY因为与独立,所以{0,1}PXXY0PX{1}PXY即a1()3a()ab11136ab联立得到11,.36ab概率论二、选择题1.已知相互独立,且分布律为1X2、X(1,2)iiX011212P那么下列结论正确的是_____.12.AXX12.{}1BPXX12.{}12CPXX.D以上都不正确C概率论12{}XX解12{0,0}XX12{1,1}XX因为相互独立,1X2、X所以1212{0,0}00PXXPXPX141212{1,1}11PXXPXPX14故12{}12PXX概率论2.,XY设离散型随机变量的联合分布律为P(,)XY(1,1)α16(1,2)(1,3)(2,1)(2,2)(2,3)1911813β且相互独立,则_______.X、Y.29,19Aαβ.19,29Bαβ.16,16Cαβ.815,118DαβA概率论解所以{1,3}PXY1PX{3}PY即118111()69181()18β因为相互独立,X、Y又因为故29α1111169183αβ解得19β13αβ或者概率论3.设211~,,XNμσ222~,,YNμσ那么的联合分布为_____..A二维正态分布,且0ρ.B二维正态分布,且不定ρ未必是二维正态分布.C.D以上都不对212221122122212211(),exp2121()()()2xμfxyσρπσσρxμyμxμρσσσC当相互独立时,则的联合分布为.X、YAX和YXY和概率论三、解答题1.把一枚均匀硬币抛掷三次,设X为三次抛掷中正面出现的次数,而Y为正面出现次数与反面出现次数之差的绝对值,求(X,Y)的分布律与边缘分布.(X,Y)可取值(0,3),(1,1),(2,1),(3,3)P{X=0,Y=3}P{X=1,Y=1}P{X=2,Y=1}P{X=3,Y=0}YX1301838001233800182311221231122231218.=3/8=3/831218解概率论P{X=0}=P{X=1}=P{X=2}=P{X=3}=P{Y=1}=P{Y=3}==1/...