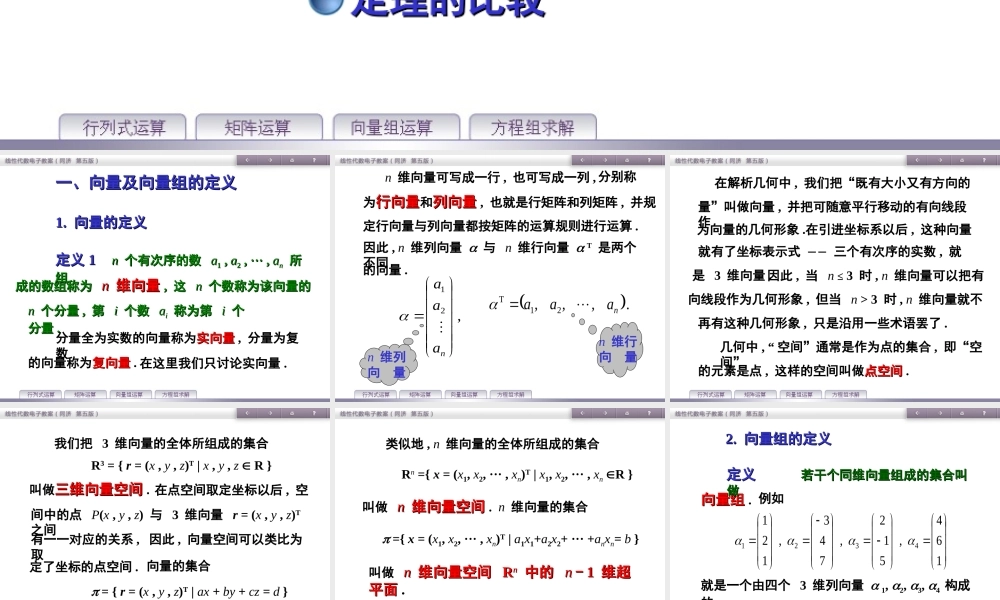
第四章向量组的线性相关第四章向量组的线性相关性性第一节向量组及其线性第一节向量组及其线性组合组合向量及向量组的定义向量及向量组的定义主要内容主要内容向量组等价向量组等价向量组等价的条件向量组等价的条件定理的比较定理的比较定义定义11nn个有次序的数个有次序的数aa11,,aa22,,······,,aann所所组组成的数组称为成的数组称为nn维向量维向量,,这这nn个数称为该向量的个数称为该向量的nn个分量个分量,,第第ii个数个数aaii称为第称为第ii个个分量分量..分量全为实数的向量称为实向量实向量,分量为复数的向量称为复向量复向量.在这里我们只讨论实向量.一、向量及向量组的定义一、向量及向量组的定义1.1.向量的定义向量的定义,21naaa.21Tna,,a,an维列向量n维行向量n维向量可写成一行,也可写成一列,为行向量行向量和列向量列向量,也就是行矩阵和列矩阵,并规定行向量与列向量都按矩阵的运算规则进行运算.因此,n维列向量与n维行向量T是两个不同的向量.分别称在解析几何中,我们把“既有大小又有方向的量”叫做向量,并把可随意平行移动的有向线段作为向量的几何形象.在引进坐标系以后,这种向量就有了坐标表示式三个有次序的实数,就因此,当n≤3时,n维向量可以把有是3维向量.向线段作为几何形象,但当n>3时,n维向量就不再有这种几何形象,只是沿用一些术语罢了.几何中,“空间”通常是作为点的集合,即“空间”的元素是点,这样的空间叫做点空间点空间.我们把3维向量的全体所组成的集合R3={r=(x,y,z)T|x,y,zR}叫做三维向量空间三维向量空间.在点空间取定坐标以后,空间中的点P(x,y,z)与3维向量r=(x,y,z)T之间有一一对应的关系,因此,向量空间可以类比为取向量的集合定了坐标的点空间.={r=(x,y,z)T|ax+by+cz=d}也叫做向量空间向量空间RR33中的平面中的平面.类似地,n维向量的全体所组成的集合Rn={x=(x1,x2,···,xn)T|x1,x2,···,xnR}叫做nn维向量空间维向量空间.n维向量的集合={x=(x1,x2,···,xn)T|a1x1+a2x2+···+anxn=b}叫做nn维向量空间维向量空间RRnn中的中的nn--11维超维超平面平面.2.2.向量组的定义向量组的定义向量组向量组.164,512,743,1214321就是一个由四个3维列向量1,2,3,4构成的定义定义若干个同维向量组成的集合叫若干个同维向量组成的集合叫做做向...