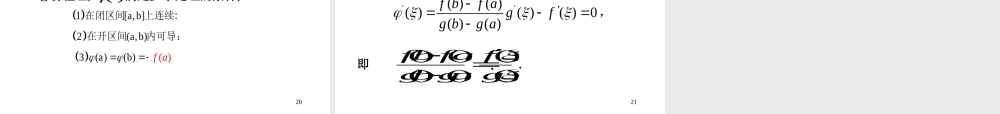第一节 微分中值定理(1).pptVIP免费

1微分中值定理和导数的应用第四章2微分中值定理的核心是拉格朗日(Lagrange)中值定理，费马定理是它的预备定理，罗尔定理是它的特例，柯西定理是它的推广。1.预备定理——费马(Fermat)定理.0)()(),()(000xfxxfxbaxf可导，则在点且取得最值，内一点在若函数费马（Fermat，1601-1665），法国人，与笛卡尔共同创立解析几何。因提出费马大、小定理而著名于世。第一节微分中值定理3xyo)(xfy12几何解释:1.预备定理——费马(Fermat)定理.0)()(),()(000xfxxfxbaxf可导，则在点且取得最值，内一点在若函数曲线在最高点或最低点如果有切线，则切线必然是水平的。4证明:达到最大值证明。在只就0)(xxf),()(,),()(0000xfxxfbaxxxxf就有内在达到最大值，所以只要在由于,0)()(00xfxxf即;0,0)()(00时当从而xxxfxxf;0,0)()(00时当xxxfxxf0)()(lim)(000x0xxfxxfxf这样.0)()(lim)(000x0xxfxxfxf.0)(0xf所以可导，在点而0)(xxf极限的保号性52.罗尔(Rolle)定理xOyCabyf(x)AB几何解释:如果连续光滑的曲线yf(x)在端点A、B处的纵坐标相等。那么，在曲线弧上至少有一点C(,f())，曲线在C点的切线是水平的。如果函数yf(x)满足条件：(1)在闭区间[a,b]上连续，(2)在开区间(a,b)内可导，(3)f(a)f(b)，则至少存在一点(a,b)，使得f()0。6证.)1(mM若,],[)(连续在baxf.mM和最小值必有最大值.)(Mxf则.0)(xf由此得),,(ba.0)(f都有.)2(mM若),()(bfaf.)(),(Mfba使，则不妨设由费马引理,.0)(f所以最大值和最小值不可能同时在端点取得。7注意：f(x)不满足条件(1)f(x)不满足条件(3)f(x)不满足条件(2)BxOyAabxOyABabcxOyABab如果定理的三个条件有一个不满足，则定理的结论就可能不成立。8例1验证2()x43[0,4]Rfxxoll验证函数在闭区间满足定理的条件，并求出定理中的1[a,b]在闭区间上连续:2(a,b)在开区间内可导：初等函数在定义区间(-,+)连续,特别在[0,4]连续'f()24xx3f(a)f(b)：f(0)=f(4)=3'f()0解方程：2-40=29例2试证方程恰有一个实根3f()xxxC证明：3231limf()1xCxxxxA,=1>0对根据极限的定义，于3231limf()1xCxxxx1110,xf()1,(2)1.MMxfM当时，特别2210,x<-f()1,(2)1.MMxfM...