第三节 函数的单调性(2).pptVIP免费

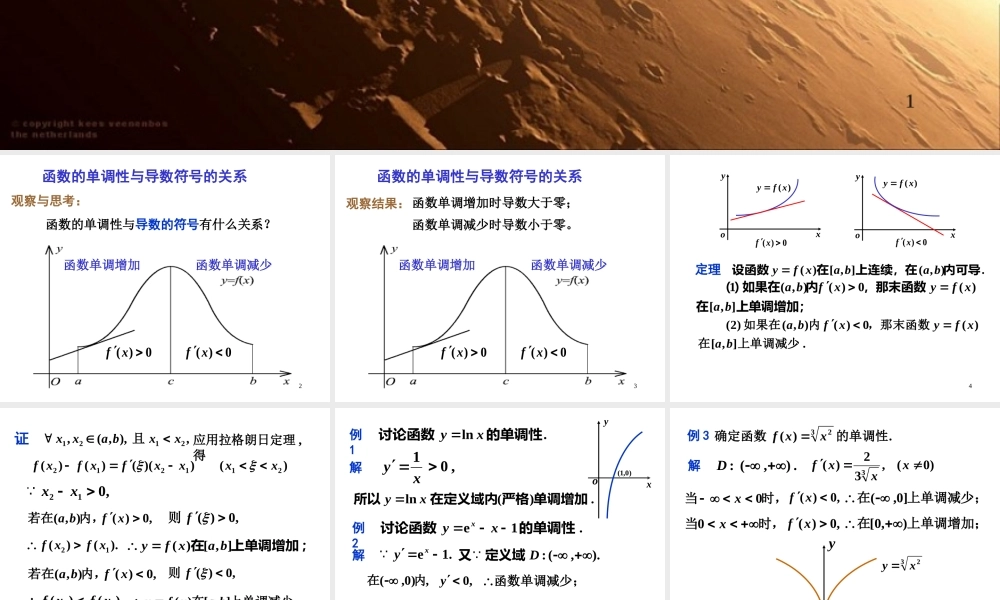
1第三节2函数的单调性与导数符号的关系观察与思考：函数单调增加函数单调减少函数的单调性与导数的符号有什么关系？0)(xf0)(xf3函数单调增加时导数大于零；观察结果：函数的单调性与导数符号的关系函数单调增加函数单调减少0)(xf0)(xf函数单调减少时导数小于零。4xyo)(xfyxyo)(xfy0)(xf0)(xf定理.),(],[)(内可导上连续，在在设函数babaxfy上单调增加；在，那末函数内如果在）（],[)(0)(),(1baxfyxfba.],[)(0)(),()2(上单调减少在，那末函数内如果在baxfyxfba5证),,(,21baxx,21xx且应用拉格朗日定理,得)())(()()(211212xxxxfxfxf,012xx,0)(),(xfba内，若在,0)(f则).()(12xfxf；上单调增加在],[)(baxfy,0)(),(xfba内，若在,0)(f则).()(12xfxf.],[)(上单调减少在baxfy6例1解.ln的单调性讨论函数xy.1exy,)0,(内在,0y函数单调减少；,),0(内在,0y.函数单调增加).,(:D定义域又例2.1e的单调性讨论函数xyxxy1,0.)(ln单调增加严格在定义域内所以xy解)0,1(xyo7例3解.)(32的单调性确定函数xxf.),(:D)0(,32)(3xxxf时，当0x,0)(xf上单调增加；在),0[时，当x0,0)(xf上单调减少；在]0,(32xyxoy8例4解.31292)(23的单调区间确定函数xxxxf).,(:D12186)(2xxxf，)2)(1(6xx得，解方程0)(xf.2,121xx时，当1x,0)(xf上单调增加；在]1,(时，当21x,0)(xf上单调减少；在]2,1[时，当x2,0)(xf上单调增加；在),2[9也可用列表的方式，x]1,(]2,1[),2[yy例4解.31292)(23的单调区间确定函数xxxxf).,(:D12186)(2xxxf，)2)(1(6xx得，解方程0)(xf.2,121xx10.,)(内导数的符号然后判断区间的定义区间数分函用驻点及不可导点来划xf导数等于零的点和不可导点，可能是单调区间的分界点．方法:注意:区间内个别点导数为零,不影响区间的单调性.例如,,3xy.),(上严格单调增加但在,032xy称驻点,0)0(yxyo11例5证.)1ln(,0成立试证时当xxx),1ln()(xxxf设.1)(xxxf则,0)(,),0(,),0[)(xfxf且上可导在上连续在；上单调增加在),0[)(xf,0)0(f而时，当0x,0)(...