第二节 微积分基本定理(1).pptVIP免费

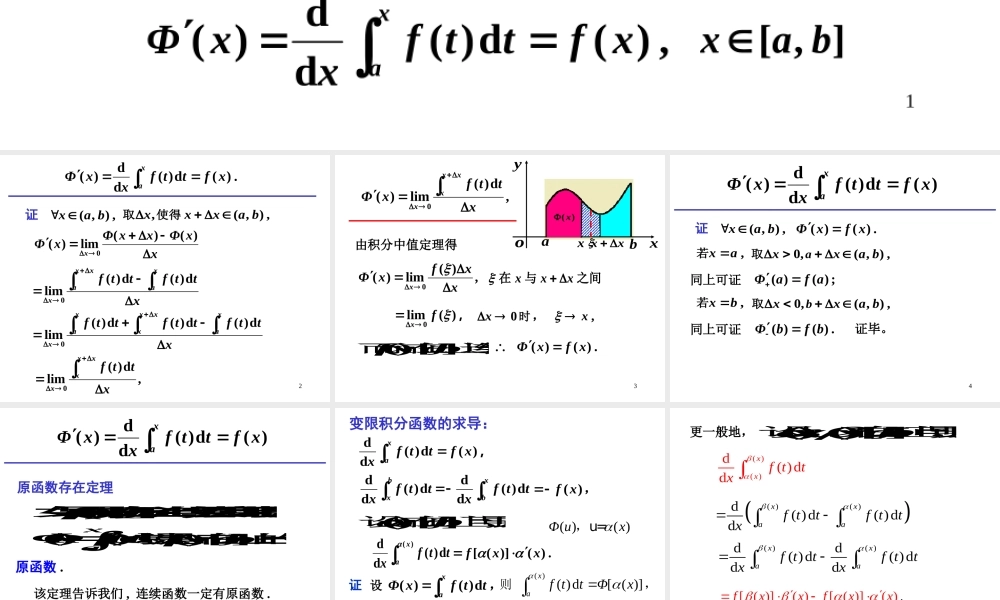
1第二节微积分基本定理用定义求定积分多数情况下是行不通的,下面介绍计算定积分的新方法.定理1设函数)(xf在],[ba上连续,则变上限积分xattfxΦd)()(],[bax在[],ab上可导,且,)(d)(dd)(xfttfxxΦxa一、原函数存在定理2证,),(baxxxΦxxΦxΦx)()(lim)(0.)(d)(dd)(xfttfxxΦxaxttfttfxaxxaxd)(d)(lim0,d)(lim0xttfxxxxxttfttfttfxaxxxxaxd)(d)(d)(lim0,),(,baxxx使得取3abxyoxx)(xx,d)(lim)(0xttfxΦxxxx由积分中值定理得之间与在xxx，时0x，)(lim0fx.)()(xfxΦ,)(lim)(0xxfxΦx而)(xf在],[ba上连续,,x4,),(bax证.)()(xfxΦ,ax若,),(,0baxxa取同上可证;)()(afaΦ,bx若,),(,0baxxb取同上可证.)()(bfbΦ证毕。)(d)(dd)(xfttfxxΦxa5原函数存在定理如果)(xf在],[ba上连续，则变上限积分函数该定理告诉我们,连续函数一定有原函数.)(d)(dd)(xfttfxxΦxattfxΦxad)()(就是)(xf在],[ba上的一个原函数.6，)(d)(ddxfttfxxabxttfxd)(dd)(d)(ddxattfx.)()]([xxf变限积分函数的求导：xbttfxd)(dd，)(xf设)(x在],[ba上可导,则，设xattfxΦd)()(证()()d[()]xafttΦx则，)(d)(ddxattfx所以)()]([xxΦ.)()]([xxf()()Φux，u=7更一般地，设)(x，)(x在],[ba上可导,则()()d()ddxxfttx[()]()[.()]()fxxfxx()()d()d()ddxxaafttfttx()()dd()d()dddxxaafttfttxx82d)(ddxattfx.2)(2xxf例1求下列变限积分函数的导数.,dsin)(1xttxf;sin)(xxf,d1)(22xttxf;1)(2xxf32d)(ddxxttfx.2)(3)(223xxfxxf,de)(sin12xttxf;cose)(2sinxxfx9设)(xf为连续函数,,d)()(ln1xxttfxF则)(xF.)1(1)(ln12xfxxfx例2)(lnxf)1(x)1(xf)1(2x10例3求下列极限.2021d)(arctanlim)1(xttxx分析：这是型未定式，应用洛必达法则.221)(arctanlimxxxx原式.42解11例3求下列极限.2200cosd(2)limsinxxttxx00分析：这是型未定式，20202dcoslimxttxx原式.1解等价无穷小替换40coslim2xxx40coslimxx220202...