6.6.1,6.6.2 矩阵函数及其计算.pdfVIP免费

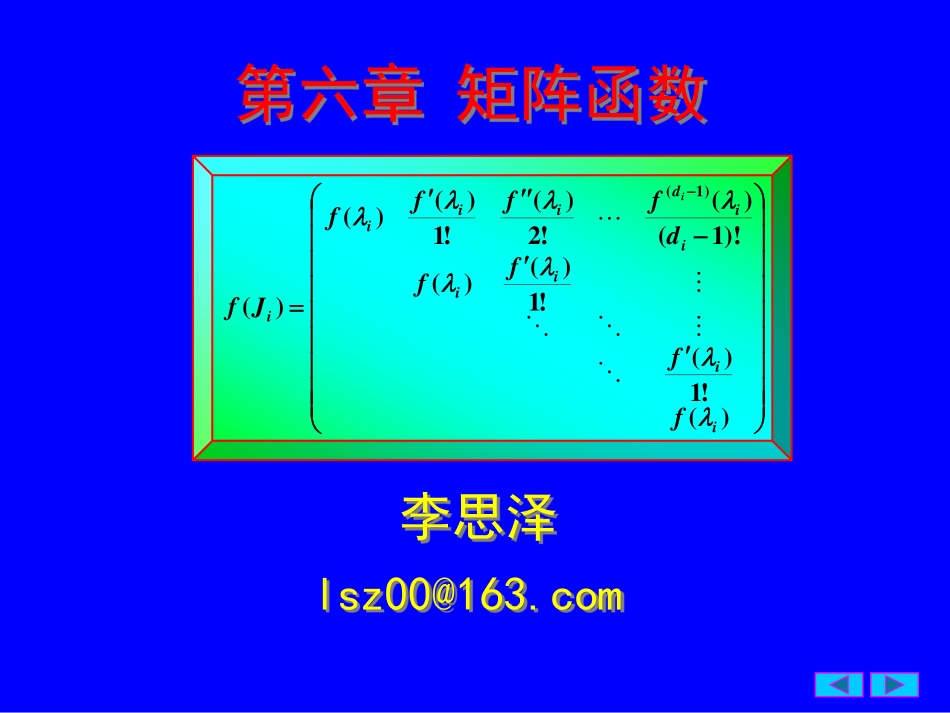
第六章矩阵函数李思泽lsz00@163.com′′−′′′=−)(!1)(!1)()()!1()(!2)(!1)()()()1(iiiiiidiiiiffffdffffJfiλλλλλλλλ2第六章矩阵函数最小多项式矩阵函数的定义矩阵函数的计算化零多项式第六章矩阵函数3矩阵函数第六章矩阵函数设关于λ的多项式,)(0111aaaapmmmm++++=−−λλλλ对矩阵,CnnA×∈则称EaAaAaAaApmmmm0111)(++++=−−)C(nn×∈是A的矩阵多项式.例设45)(23++=λλλf1)若1−=PJPA:)(1−=PPJAkk则EAAAf45)(23++=1121345−−−++=PEPPPJPPJ123)45(−++=PEJJP1)(−=PJPf2)若:21=JJJ则则EJJJf45)(23++=321=JJ2215+JJ++++=22232121314545EJJEJJ+214EE=)()(21JfJf4矩阵函数第六章矩阵函数例设45)(23++=λλλf1),1−=PJPA1)()(−=PJPfAf2),21=JJJ=)(Jf3)对:11=λλλJ则+=01010λλλJBE+=λ,00010001001022==B.03=BkkBEJ)(+=λ22211EBCEBCEkkkkk−−++=λλλ−=−−−kkkkkkkkkkλλλλλλ1212)1()()(21JfJfEJJJf45)(23++==32323333λλλλλλ+2222125λλλλλ+1114′′′′=)(!1/)()(!2/)(!1/)()(λλλλλλffffff4)Aα=λα,则A2α=λ2α,f(A)α=f(λ)α.5结论为A的Jordan标准形,1)设多项式,)(01aaafmm+++=λλλJAPP=−1=sJJ1则1)()(−=PJfPAf,)()(11−=PJfJfPs,)(!1)(!1)()()!1()(!2)(!1)()()()1(′′−′′′=−iiiiiidiiiiffffdffffJfiλλλλλλλλ其中iJ是对角线上元为λi的di阶Jordan块.第六章矩阵函数矩阵函数,11idiiiiJ=λλλ2)f(A)的特征值为f(λi),其中λi为A的特征值.6定义6.1.1.设矩阵函数若多项式,CnnA×∈满足,)(nnOAp×=定义已知,CnnA×∈在A的化零多项式中,次数最低且首项系数为1的化零多项式称为A的最小多项式,记为).(λψA性质(2)矩阵A的最小多项式是唯一的.(1)矩阵的任何一个化零多项式均能被)(λψA整除.(3)相似矩阵有相同的最小多项式.问题:如何求一...