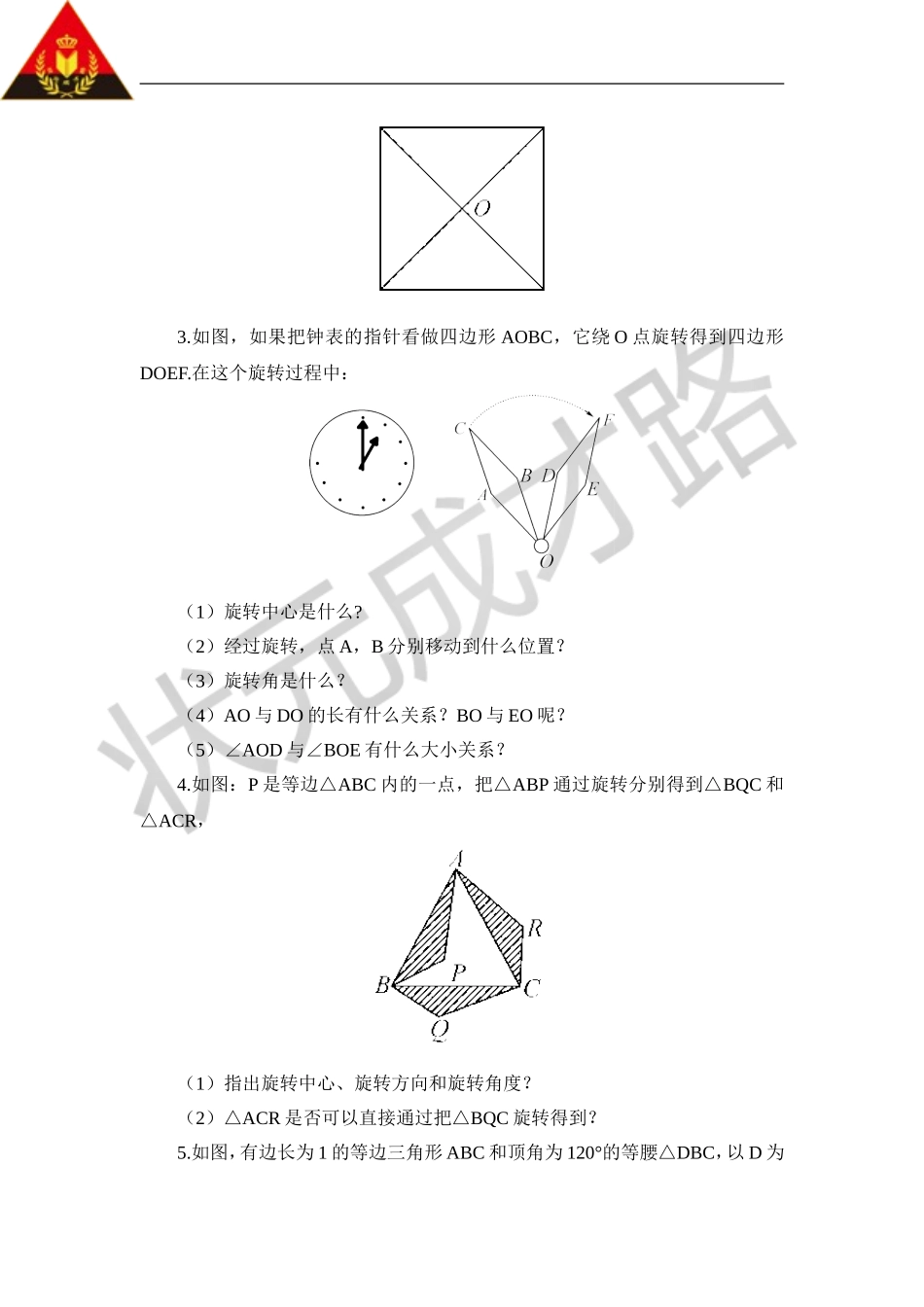
2.旋转的特征【知识与技能】通过具体实例认识旋转,理解旋转前后两个图形的对应点到旋转中心的距离相等,对应点与旋转中心的连线所成的角彼此相等的性质,能够按照要求作出简单平面图形旋转后的图形.【过程与方法】通过对日常生活中与旋转现象有关的图形探索过程,掌握相关画图的操作能力,发展审美观.【情感态度】培养识图能力,体会旋转现象在现实生活中的价值.【教学重点】图形的旋转的基本性质及其应用.【教学难点】图形的旋转的基本性质及其应用.一、情境导入,初步认识1.什么叫旋转?什么叫旋转中心?什么叫旋转角?2.什么叫旋转的对应点?【教学说明】复习上节课的内容,为本节课的学习做铺垫.二、思考探究,获取新知1.如图,若旋转中心在△ABC的外面点O处,逆时针转动60°,将整个△ABC旋转到△A′B′C′的位置.观察上图,探索图中线段之间与角之间的关系,填空.旋转中心是点O,点A、B、C都是绕着点O旋转60°角到对应点A′、B′、C′,则OA=,OB=,OC=,AB=,BC=,CA=,∠CAB=,∠ABC=,∠BCA=.∠AOA′===60°△ABC和△A′B′C′的形状、大小有何变化?.你发现了什么?2.(1)将一个平面图形F上的每一点,绕这个平面一点旋转,得到图形F′,图形的这种变换就叫做旋转.(2)对应点到对应中心的距离.(3)对应点与旋转中心所成的角彼此,且等于角.(4)旋转不改变图形的和.【归纳结论】图中每一点都绕着旋转中心按同一旋转方向旋转了同样的角度;对应点到旋转中心的距离相等;对应线段长度相等,对应角相等;对应点与旋转中心的连线所成的角彼此相等;图形的形状与大小不变.【教学说明】通过观察图形,让学生自己总结规律,锻炼学生的归纳概括能力.三、运用新知,深化理解1.下列关于旋转和平移的说法正确的是()A.旋转使图形的形状发生改变B.由旋转得到的图形一定可以通过平移得到C.平移与旋转的共同之处是改变图形的位置和大小D.对应点到旋转中心距离相等2.如图把正方形绕着点O旋转,至少要旋转度后与原来的图形重合.3.如图,如果把钟表的指针看做四边形AOBC,它绕O点旋转得到四边形DOEF.在这个旋转过程中:(1)旋转中心是什么?(2)经过旋转,点A,B分别移动到什么位置?(3)旋转角是什么?(4)AO与DO的长有什么关系?BO与EO呢?(5)∠AOD与∠BOE有什么大小关系?4.如图:P是等边△ABC内的一点,把△ABP通过旋转分别得到△BQC和△ACR,(1)指出旋转中心、旋转方向和旋转角度?(2)△ACR是否可以直接通过把△BQC旋转得到?5.如...