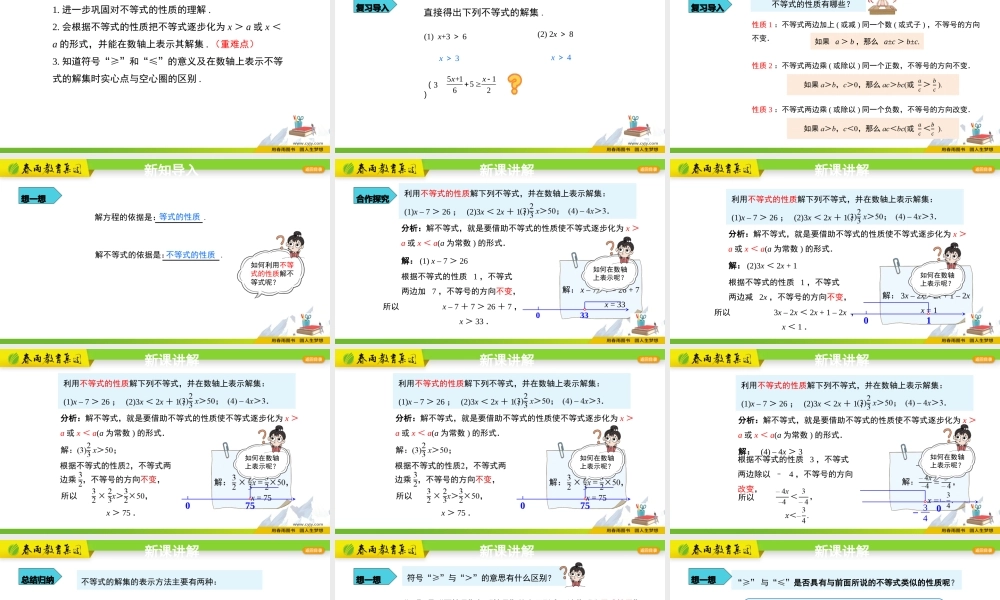
9.1.2不等式的性质第2课时人教版七年级下人教版同步课件1.进一步巩固对不等式的性质的理解.2.会根据不等式的性质把不等式逐步化为x>a或x<a的形式,并能在数轴上表示其解集.(重难点)3.知道符号“≥”和“≤”的意义及在数轴上表示不等式的解集时实心点与空心圈的区别.学习目标直接得出下列不等式的解集.(1)x+3>6(2)2x>8x>3x>45+11562xx(3)复习导入新知导入不等式的性质有哪些?性质1:不等式两边加上(或减)同一个数(或式子),不等号的方向不变.如果a>b,那么a±c>b±c.性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变.性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.复习导入新知导入如何利用不等式的性质解不等式呢?解方程的依据是:.等式的性质解不等式的依据是:.不等式的性质想一想新知导入(1)x–7>26;(2)3x<2x+1;利用不等式的性质解下列不等式,并在数轴上表示解集:分析:解不等式,就是要借助不等式的性质使不等式逐步化为x>a或x<a(a为常数)的形式.根据不等式的性质1,不等式两边加7,不等号的方向不变,x>33.所以x–7+7>26+7,x–7=26解:x–7+7=26+7x=33解:(1)x–7>26如何在数轴上表示呢?033合作探究新课讲解分析:解不等式,就是要借助不等式的性质使不等式逐步化为x>a或x<a(a为常数)的形式.根据不等式的性质1,不等式两边减2x,不等号的方向不变,x<1.所以3x–2x<2x+1–2x,3x=2x+1解:3x–2x=2x+1–2xx=1解:(2)3x<2x+1如何在数轴上表示呢?01(1)x–7>26;(2)3x<2x+1;利用不等式的性质解下列不等式,并在数轴上表示解集:新课讲解x=75分析:解不等式,就是要借助不等式的性质使不等式逐步化为x>a或x<a(a为常数)的形式.x>75.如何在数轴上表示呢?075(1)x–7>26;(2)3x<2x+1;利用不等式的性质解下列不等式,并在数轴上表示解集:新课讲解x=75分析:解不等式,就是要借助不等式的性质使不等式逐步化为x>a或x<a(a为常数)的形式.x>75.如何在数轴上表示呢?075(1)x–7>26;(2)3x<2x+1;利用不等式的性质解下列不等式,并在数轴上表示解集:新课讲解–4x=3分析:解不等式,就是要借助不等式的性质使不等式逐步化为x>a或x<a(a为常数)的形式.根据不等式的性质3,不等式两边除以–4,不等号的方向改变,所以解:(4)–4x>3如何在数轴上表示呢?0–34(1)x–7>26;(2)3x<2x+1;利用不等式的性质解下列不等式,并在数轴上表示解集:新课讲解不等式的...