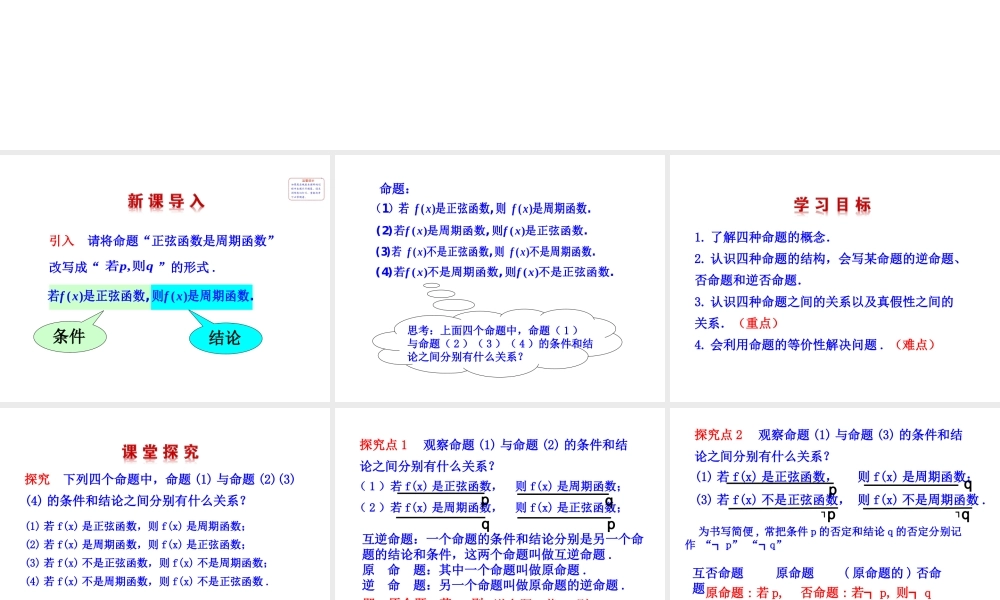
1.1.2四种命题引入请将命题“正弦函数是周期函数”改写成“”的形式.,pq若则条件结论()()fxfx若是正弦函数,则是周期函数.()()fxfx(2)若是周期函数,则是正弦函数.()()fxfx(3)若不是正弦函数,则不是周期函数.命题:思考:上面四个命题中,命题(1)与命题(2)(3)(4)的条件和结论之间分别有什么关系?()()fxfx(1)若是正弦函数,则是周期函数.()()fxfx(4)若不是周期函数,则不是正弦函数.1.了解四种命题的概念.2.认识四种命题的结构,会写某命题的逆命题、否命题和逆否命题.3.认识四种命题之间的关系以及真假性之间的关系.(重点)4.会利用命题的等价性解决问题.(难点)探究下列四个命题中,命题(1)与命题(2)(3)(4)的条件和结论之间分别有什么关系?(1)若f(x)是正弦函数,则f(x)是周期函数;(2)若f(x)是周期函数,则f(x)是正弦函数;(3)若f(x)不是正弦函数,则f(x)不是周期函数;(4)若f(x)不是周期函数,则f(x)不是正弦函数.(1)若f(x)是正弦函数,则f(x)是周期函数;(2)若f(x)是周期函数,则f(x)是正弦函数;互逆命题:一个命题的条件和结论分别是另一个命题的结论和条件,这两个命题叫做互逆命题.原命题:其中一个命题叫做原命题.逆命题:另一个命题叫做原命题的逆命题.pqqp即原命题:若p,则q逆命题:若q,则p例如,命题“同位角相等,两直线平行”的逆命题是“两直线平行,同位角相等”.探究点1观察命题(1)与命题(2)的条件和结论之间分别有什么关系?(1)若f(x)是正弦函数,则f(x)是周期函数;(3)若f(x)不是正弦函数,则f(x)不是周期函数.pq┐p原命题:若p,则q┐q为书写简便,常把条件p的否定和结论q的否定分别记作“┐p”“┐q”否命题:若┐p,则┐q互否命题原命题(原命题的)否命题例如,命题“同位角相等,两直线平行”的否命题是“同位角不相等,两直线不平行”.探究点2观察命题(1)与命题(3)的条件和结论之间分别有什么关系?(1)若f(x)是正弦函数,则f(x)是周期函数;(4)若f(x)不是周期函数,则f(x)不是正弦函数.pq┐q原命题:若p,则q┐p逆否命题:若┐q,则┐p互为逆否命题原命题(原命题的)逆否命题例如,命题“同位角相等,两直线平行”的逆否命题是“两直线不平行,同位角不相等”.探究点3观察命题(1)与命题(4)的条件和结论之间分别有什么关系?三个概念1.互逆命题:一般地,对于两个命题,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么我们把这样的两个命题叫做互逆命题.其中一个命题叫做原命题,另一个叫做原命题的逆命题....