【数学】2．3．1《平面向量的基本定理》课件（新人教A版必修4）.pptVIP免费

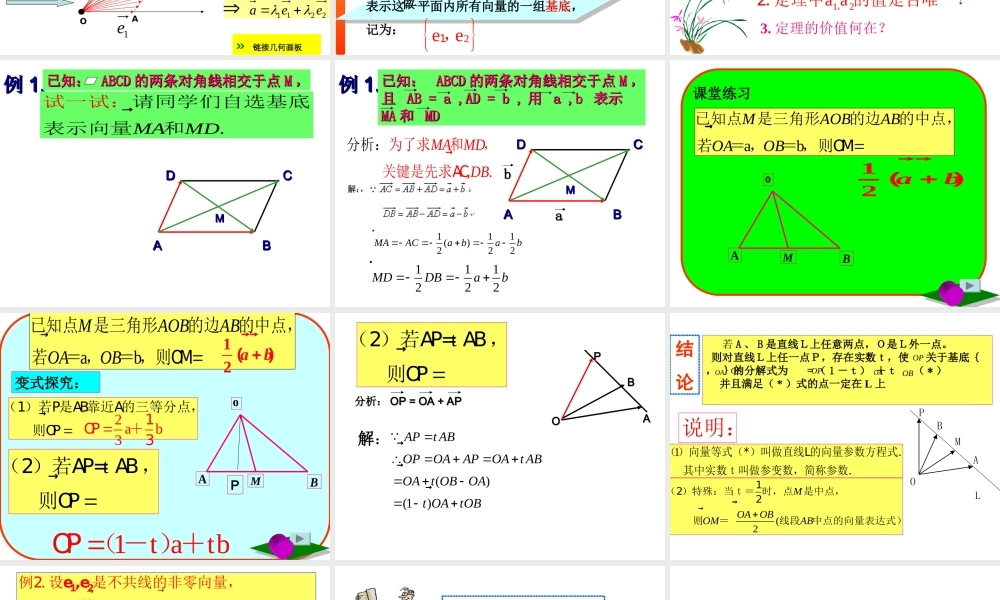
2.3.1《平面向量基本定理》教学目的•（1）了解平面向量基本定理；理解平面向量的坐标的概念；•（2）初步掌握应用向量解决实际问题的重要思想方法；•（3）能够在具体问题中适当地选取基底，使其他向量都能够用基底来表达.•教学重点：平面向量基本定理.•教学难点：平面向量基本定理的理解与应用.向量的坐标表示的理解及运算的准确性.一、问题情境（1）如何求此时竖直和水平方向速度？（2）利用什么法则？vsinvcosvBAMN2e�1e�探究：给定平面内两个向量、，平面内任一向量是否都可以在这两向量方向上分解呢？�1e�2e分解平移共同起点1e2ea1e1e2eaa2eOABOBOAa11eOA22eOB2211eea»链接几何画板平面向量基本定理如果,是同一平面内的两个不共线的向量，那么对于这一平面内的任意向量，存在唯一一对实数、，使�1e�2eaa1a2aa��1122a=e+e我们把不共线的向量，叫做表示这一平面内所有向量的一组基底，记为：�1e�2e2ee1，如果,是同一平面内的两个不共线的向量，那么对于这一平面内的任意向量，存在唯一一对实数、，使�1e�2eaa1a2aa��1122a=e+e»探究定理内涵1.基底、条件：1e2e基底组数：不共线向量无数组3.定理的价值何在？12aa，2.定理中的值是否唯一？例例1.1.已知：已知：ABCDABCD的两条对角线相交于点的两条对角线相交于点MM，，MMBBAACCDD.MAMD�请同学们自选基底表示向量和试一试：例例1.1.已知：已知：ABCDABCD的两条对角线相交于点的两条对角线相交于点MM，，且且AB=a,AD=b,AB=a,AD=b,用用a,ba,b表示表示MAMA和和MDMDMMBBAACCDDbbaa.MAMDDB��为了求和，关键是先求AC,分析：111()222MAACabab�111222MDDBab�课堂练习oABM12ab（）abMAOBABOAOB�已知点是三角形的边的中点，若＝，＝，则OM变式探究：oABM�（1）若P是AB靠近A的三等分点，则OPabMAOBABOAOB�已知点是三角形的边的中点，若＝，＝，则OM12ab（）Pt��（2）若AP=AB，则OP2ab3�1OP＋31tatb�OP（－）＋BBOOAAPPt��（2）若AP=AB，则OP分析：分析：OP=OA+APOP=OA+AP()(1)APtABOPOAAPOAtABOAtOBOAtOAtOB����解：结论若A、B是直线Ｌ上任意两点，Ｏ是Ｌ外一点。则对直线Ｌ上任一点Ｐ，存在实数ｔ，使关于基底｛，｝的分解式为=（1－t）＋t（*）并且满足（*）式的点一定在L上OP�OA�OB�OP�OA�OB�说明：1（）向量等式（*）叫做直线L...