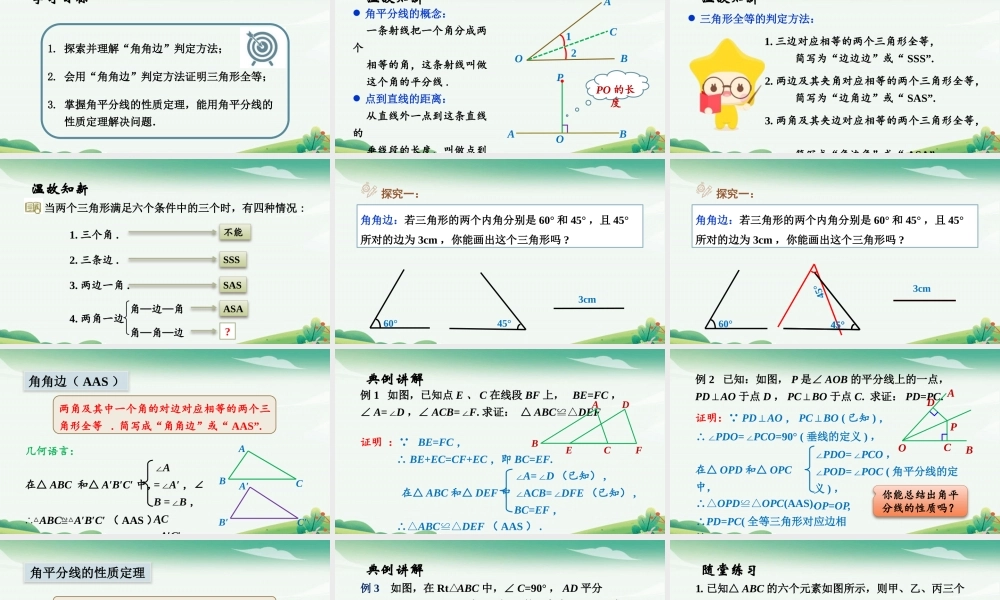
第一章三角形的初步认识1.5全等三角形的判定第4课时“角角边”与角平分线的性质学习目标1.探索并理解“角角边”判定方法;2.会用“角角边”判定方法证明三角形全等;3.掌握角平分线的性质定理,能用角平分线的性质定理解决问题.温故知新角平分线的概念:一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.点到直线的距离:从直线外一点到这条直线的垂线段的长度,叫做点到COBA12OPABPO的长度温故知新三角形全等的判定方法:1.三边对应相等的两个三角形全等,简写为“边边边”或“SSS”.2.两边及其夹角对应相等的两个三角形全等,简写为“边角边”或“SAS”.3.两角及其夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”温故知新1.三个角.2.三条边.3.两边一角.4.两角一边不能SSS当两个三角形满足六个条件中的三个时,有四种情况:SAS角—边—角角—角—边ASA?探究一:角角边:若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗?60°45°3cm60°探究一:角角边:若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗?45°45°3cm45°两角及其中一个角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.角角边(AAS)ABCA′B′C′几何语言:在△ABC和△A′B′C′中,∴△ABC≌△A′B′C′(AAS).∠A=∠A′,∠B=∠B,ACA′C′典例讲解例1如图,已知点E、C在线段BF上,BE=FC,∠A=∠D,∠ACB=∠F.求证:△ABC≌△DEF证明: BE=FC,∴BE+EC=CF+EC,即BC=EF.在△ABC和△DEF中∴△ABC≌△DEF(AAS).ABCDEF∠A=∠D(已知),∠ACB=∠DFE(已知),BC=EF,例2已知:如图,P是∠AOB的平分线上的一点,PD⊥AO于点D,PC⊥BO于点C.求证:PD=PC.证明: PD⊥AO,PC⊥BO(已知),∴∠PDO=∠PCO=90°(垂线的定义),∠PDO=∠PCO,∠POD=∠POC(角平分线的定义),OP=OP,∴PD=PC(全等三角形对应边相等在△OPD和△OPC中,∴△OPD≌△OPC(AAS).DPAOBC你能总结出角平分线的性质吗?角平分线上的点到角两边的距离相等.角平分线的性质定理几何语言: OC是∠AOB的平分线,且PD⊥OA,PE⊥OB,∴PD=PEEDOABPC典例讲解例3如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,BD=2CD,点D到AB的距离为5.6cm,求BC的长.解:过点D作DE⊥AB于点E. ∠C=90°,AD平分∠CAB(已知),∴CD=DE=5.6cm.(角平分线上的点到角两边的距离相等)EACDB随堂练习1.已知△ABC的六个元素如图所示,则甲、乙、丙...