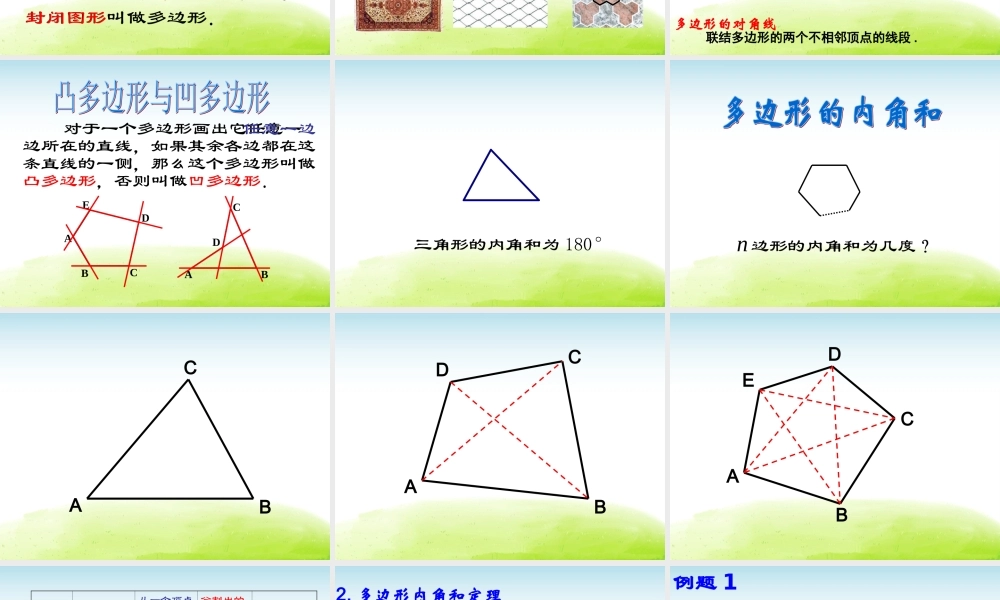
22.1多边形教学目标:教学重点:1.知道多边形的定义及其边、顶点、对角线等概念,会判断一个多边形是否是凸多边形.2.经历探索多边形内角和定理的过程,掌握多边形内角和定理,会运用定理进行有关计算.3.初步感受化归、类比、从特殊到一般等数学思想,发展合情推理意识,提高主动探索能力.多边形内角和定理的探索、归纳及运用定理进行简单计算.通过动手实践、观察分析、探索并归纳多边形内角和定理.教学难点:教材分析学情分析本节课由复习学生极为熟悉的三角形入手,引出多边形的概念,然后介绍多边形的边、顶点等多边形的基本元素,接着分清凹多边形和凸多边形。最后通过动手实践、观察分析、探索并归纳多边形内角和定理.经历探索多边形内角和定理的过程,掌握多边形内角和定理,会运用定理进行有关计算.本节课重点研究多边形,由于之前对三角形极为熟悉,因此本节课通过复习三角形入手,引出多边形的概念,以及通过三角形的内角和来动手实践、观察分析、探索并归纳多边形内角和定理.这样处理学生容易掌握。三角形四边形五边形……由平面内不在同一直线上的三条线段首尾顺次联结所组成的封闭图形叫做三角形.三角形四边形五边形……由平面内不在同一直线上的一些线段首尾顺次联结所组成的封闭图形叫做多边形.不在同一直线上首尾顺次联结封闭图形1.多边形的内角和多边形由平面内不在同一直线上的一些线段首尾顺次联结所组成的封闭图形叫做多边形.多边形的边组成多边形的每一条线段叫做多边形的边.多边形的顶点相邻的两条线段的公共端点叫做多边形的顶点.多边形的对角线多边形相邻两边所成的角叫做多边形的内角.多边形的内角联结多边形的两个不相邻顶点的线段.对于一个多边形画出它任意一边所在的直线,如果其余各边都在这条直线的一侧,那么这个多边形叫做凸多边形,否则叫做凹多边形.BACDEDABC任意一边三角形的内角和为180°边形的内角和为几度?nABCABCDABCDE多边形的边数图形从一个顶点出发的对角线条数分割出的三角形的个数多边形的内角和456nn-2232×180º3×180º(n-2)×180º12n-3……………44×180º32.多边形内角和定理n边形的内角和等于(n-2)180°例题1求十边形的内角和.例题2已知一个多边形的内角和等于2160°,求这个多边形的边数.作业布置习题22.1(1)通过本节课的学习你有什么收获?学习本节课你有什么感受?请同学们畅所欲言.资料来源:3A备课网--整册备课资料打包下载http://www.3abeike.com/