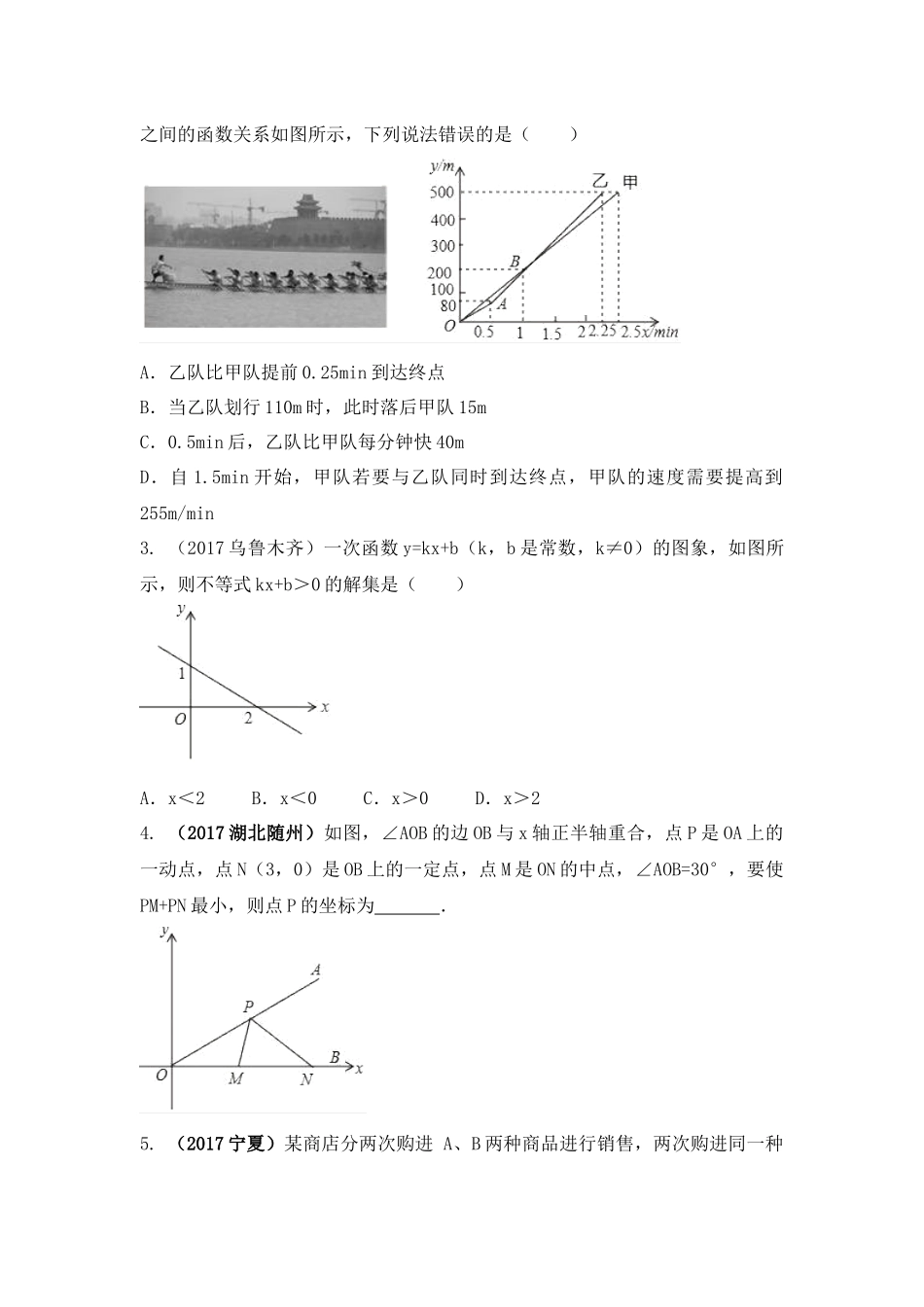
第十二讲一次函数的综合应用1.一次函数和一元一次方程的关系一次函数y=kx+b的函数值为0时,相应的自变量的值即为方程kx+b=0的;若从图象上来看,则可看做函数y=kx+b的图象与x轴的交点的,即为方程kx+b=0的解.2.一次函数和一元一次不等式的关系任何一元一次不等式都可以转化为类似ax+b>0或ax+b<0的形式,所以解一元一次不等式可以看做:当一次函数y=ax+b的值大(小)于0时,求自变量相应的取值范围;反之,求一次函数y=ax+b的值何时大(小)于0时,只要求出不等式ax+b>0或ax+b<0的解集即可.①如图1,一次函数y=kx+b的图象与x轴交于点(x0,0).当它在x轴上方的部分时,对应不等式为,其解为;当它在轴下方的部分时,对应不等式为,其解为.②如图2,一次函数与y2=k2x+b2的图象交点的横坐标为x0.当y2=k2x+b2的图象在y1=k1x+b1上方的部分时,对应不等式为,其解为;当y2=k2x+b2的图象在y1=k1x+b1下方的部分时,对应不等式为,其解为.3.一次函数的实际应用知识回顾(1)通过图象获取信息通过观察一次函数的图象获取有用的信息是我们在日常生活中经常遇到的问题,要掌握这个重点在于对函数图象的观察和分析,观察函数图象时,首先要看分别代表的是什么,也就是观察图象反映的是哪两个变量之间的关系.观察图象获取信息时,一定要注意图象上的特殊点,这些特殊点对我们解决问题有很大的帮助.(2)一次函数图象的应用一次函数和正比例函数是我们接触到的最简单的函数,它们的图象和性质在现实生活中有着广泛的应用.在实际问题中,当自变量的取值范围受到一定的限制时,函数y=kx+b(k≠0)的图象就不再是一条直线.要根据实际情况进行分析,其图象可能是等等.1.如图,大小两个正方形在同一水平线上,小正方形从图①的位置开始,匀速向右平移,到图③的位置停止运动.如果设运动时间为x,大小正方形重叠部分的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是()A.B.C.D.2.(2017山东聊城)端午节前夕,在东昌湖举行第七届全民健身运动会龙舟比赛中,甲、乙两队在500米的赛道上,所划行的路程y(m)与时间x(min)基础检测之间的函数关系如图所示,下列说法错误的是()A.乙队比甲队提前0.25min到达终点B.当乙队划行110m时,此时落后甲队15mC.0.5min后,乙队比甲队每分钟快40mD.自1.5min开始,甲队若要与乙队同时到达终点,甲队的速度需要提高到255m/min3.(2017乌鲁木齐)一次函数y=kx+b(k,b是常数,k≠0)的图象,...