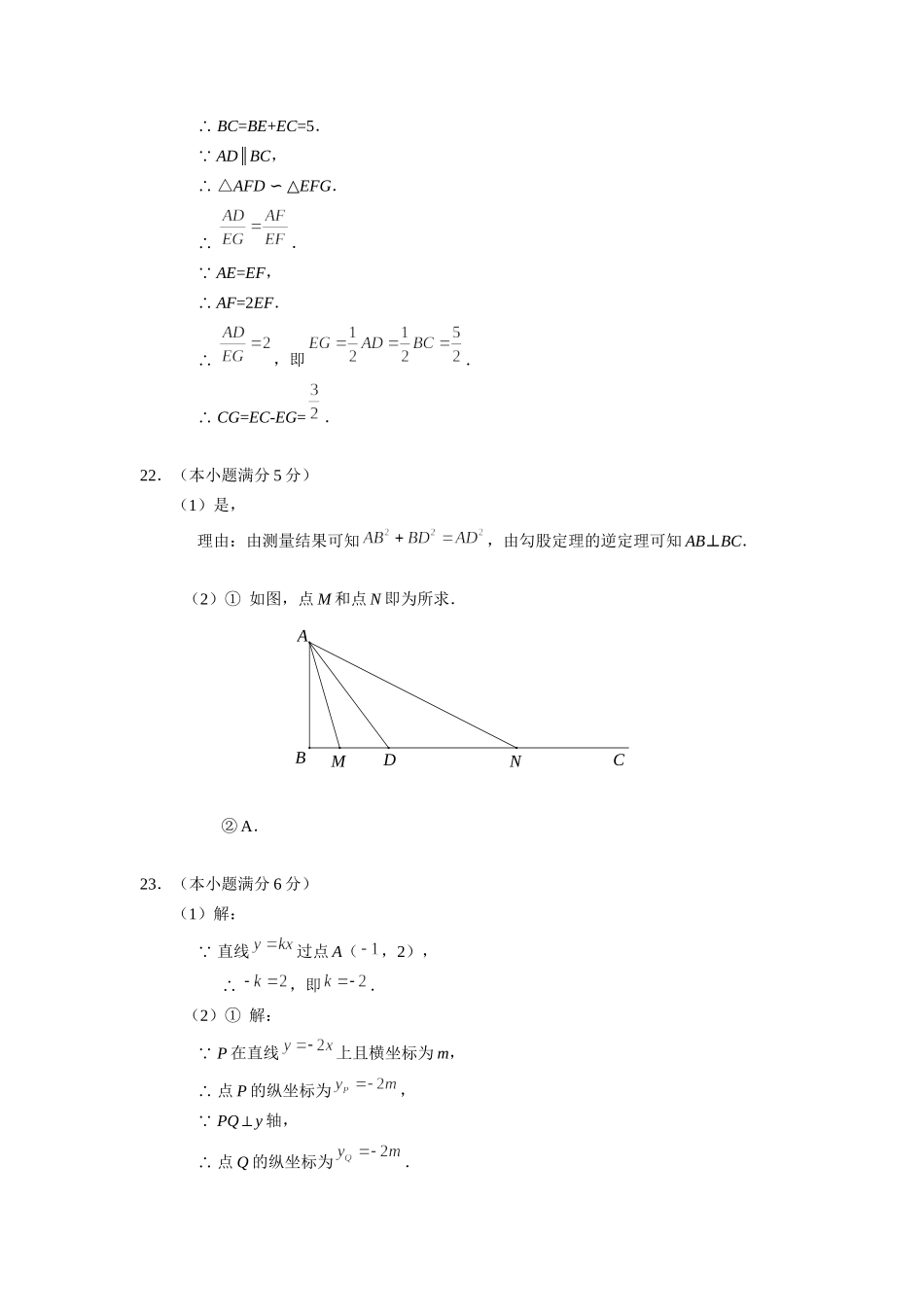
海淀区九年级第二学期期中练习数学试卷答案一、选择题(本题共16分,每小题2分)题号12345678答案ACABDCAD二、填空题(本题共16分,每小题2分)9.10.11.110°12.答案不唯一,如:13.114.2或-615.916.乙三、解答题(本题共68分,第17-20题,每小题5分,第21题6分,第22题5分,第23题6分,第24题5分,第25-26题,每小题6分,第27-28题,每小题7分)解答应写出文字说明、演算步骤或证明过程.17.(本小题满分5分)解:原式.18.(本小题满分5分)解:原不等式组为解不等式①,得.解不等式②,得.∴原不等式组的解集为.19.(本小题满分5分)证明: AB∥DE,∴∠B=∠DEF. BE=CF,∴BE+EC=CF+EC.∴BC=EF.在△ABC和△DEF中,∴△ABC≌△DEF.∴∠A=∠D.20.(本小题满分5分)解: ∴∴原式21.(本小题满分6分)(1)证明: 四边形ABCD是矩形,∴∠B=∠C=90°.∴∠BAE+∠AEB=90°. AE⊥ED,∴∠AED=90°.∴∠AEB+∠CED=90°.∴∠BAE=∠CED.∴△ABE∽△ECD.(2)解: 由(1),△ABE∽△ECD,∴. 矩形ABCD中,CD=AB=2,BE=1,∴EC=4.GFEDCBA∴BC=BE+EC=5. AD∥BC,∴△AFD∽△EFG.∴. AE=EF,∴AF=2EF.∴,即.∴CG=EC-EG=.22.(本小题满分5分)(1)是,理由:由测量结果可知,由勾股定理的逆定理可知AB⊥BC.(2)①如图,点M和点N即为所求.A②.23.(本小题满分6分)(1)解: 直线过点A(,2),∴,即.(2)①解: P在直线上且横坐标为m,∴点P的纵坐标为, PQ⊥y轴,∴点Q的纵坐标为.CNMDBA 点Q在函数()的图象上,∴点Q的横坐标为.∴点Q的坐标为(,).②24.(本小题满分5分)(1)4.36(2)②③(3)8.6125.(本小题满分6分)(1)证明:连接OC,在⊙O中 ∠BOC=2∠E,∠ABE=2∠E,∴∠BOC=∠ABE.∴AB∥OC.∴∠OCD+∠ADC=180°. AB⊥CD于点D,∴∠ADC=90°.∴∠OCD=90°.∴OC⊥CD.∴CD是⊙O的切线.(2)解:方法1:连接AC,BC, BE是⊙O的直径,∴∠BCE=90°.∴∠OBC+∠E=90°. ∠OCD=90°,∴∠OCB+∠BCD=90°. OB=OC,∴∠OCB=∠OBC.∴∠E=∠BCD.∴.DEOCBADEOCBA∴在Rt△BCD中,. ∠A=∠E,∴在Rt△ACD中,.∴.方法2:连接CD,过点O作OH⊥AB于H,设⊙O的半径为r.同方法1可得∠BCD=∠E,CD=3. OH⊥AB,∴∠OHD=90°=∠OCD=∠ADC.∴四边形OHDC是矩形.∴OH=CD=3,HD=OC=r,∴. Rt△OHB中,,∴.解得:.∴.∴由垂径定理,AB=2HB=8.26.(本小题满分6分)(1...