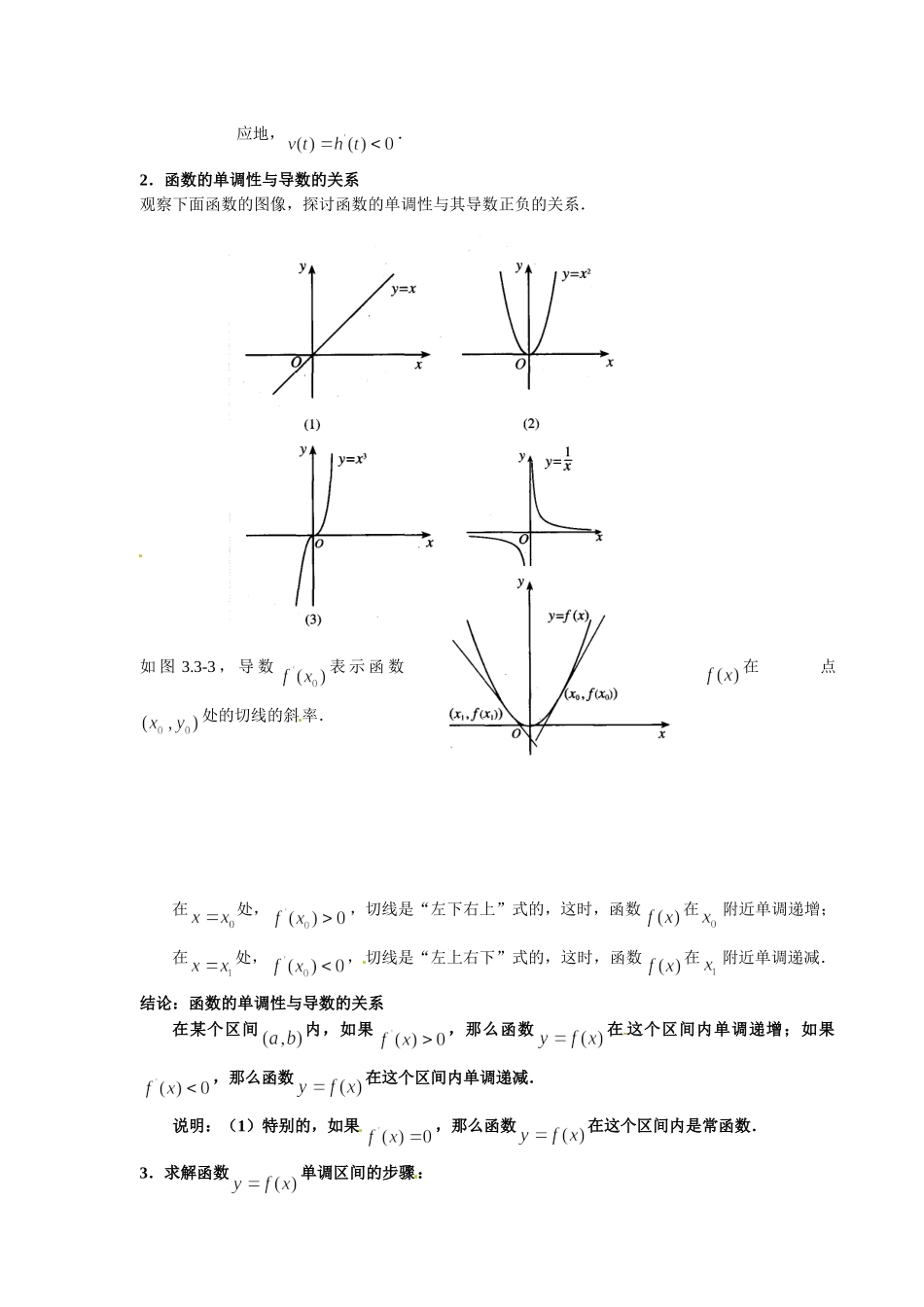
甘肃省金昌市第一中学2014年高中数学3.3.1函数的单调性与导数教案新人教A版选修1-1了解函数的单调性与导数的关系;能利用导数研究函数的单调性;会利用导数求函数的单调区间。2、过程与方法通过本节的学习,掌握用导数研究函数单调性的方法。3、情感、态度与价值观通过实例探究函数的单调性与导数的关系。通过这一过程,提高理性思维的能力。教学重难点重点:函数单调性和导数的关系;会根据导数判断函数的单调性;会利用导数求出函数的单调区间。难点:理解并掌握函数的单调性与导数的关系教学过程一、复习引入:1.常见函数的导数公式:;;;奎屯王新敞新疆奎屯王新敞新疆奎屯王新敞新疆奎屯王新敞新疆2.法则1.法则2,奎屯王新敞新疆法则3奎屯王新敞新疆二、讲授新课1.问题:图3.3-1(1),它表示跳水运动中高度随时间变化的函数的图像,图3.3-1(2)表示高台跳水运动员的速度随时间变化的函数的图像.运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?通过观察图像,我们可以发现:(1)运动员从起点到最高点,离水面的高度随时间的增加而增加,即是增函数.相应地,.(2)从最高点到入水,运动员离水面的高度随时间的增加而减少,即是减函数.相应地,.2.函数的单调性与导数的关系观察下面函数的图像,探讨函数的单调性与其导数正负的关系.如图3.3-3,导数表示函数在点处的切线的斜率.在处,,切线是“左下右上”式的,这时,函数在附近单调递增;在处,,切线是“左上右下”式的,这时,函数在附近单调递减.结论:函数的单调性与导数的关系在某个区间内,如果,那么函数在这个区间内单调递增;如果,那么函数在这个区间内单调递减.说明:(1)特别的,如果,那么函数在这个区间内是常函数.3.求解函数单调区间的步骤:(1)确定函数的定义域;(2)求导数;(3)解不等式,解集在定义域内的部分为增区间;(4)解不等式,解集在定义域内的部分为减区间.三.典例分析例1.已知导函数的下列信息:当时,;当,或时,;当,或时,试画出函数图像的大致形状.解:当时,,可知在此区间内单调递增;当,或时,;可知在此区间内单调递减;当,或时,,这两点比较特殊,我们把它称为“临界点”.综上,函数图像的大致形状如图3.3-4所示.例2.判断下列函数的单调性,并求出单调区间.(1);(2)(3);(4)解:(1)因为,所以,因此,在R上单调递增,如图3.3-5(1)所示.(2)因为,所以,当,即时,函数单...