2.4.2抛物线的简单几何性质（1）.docVIP免费

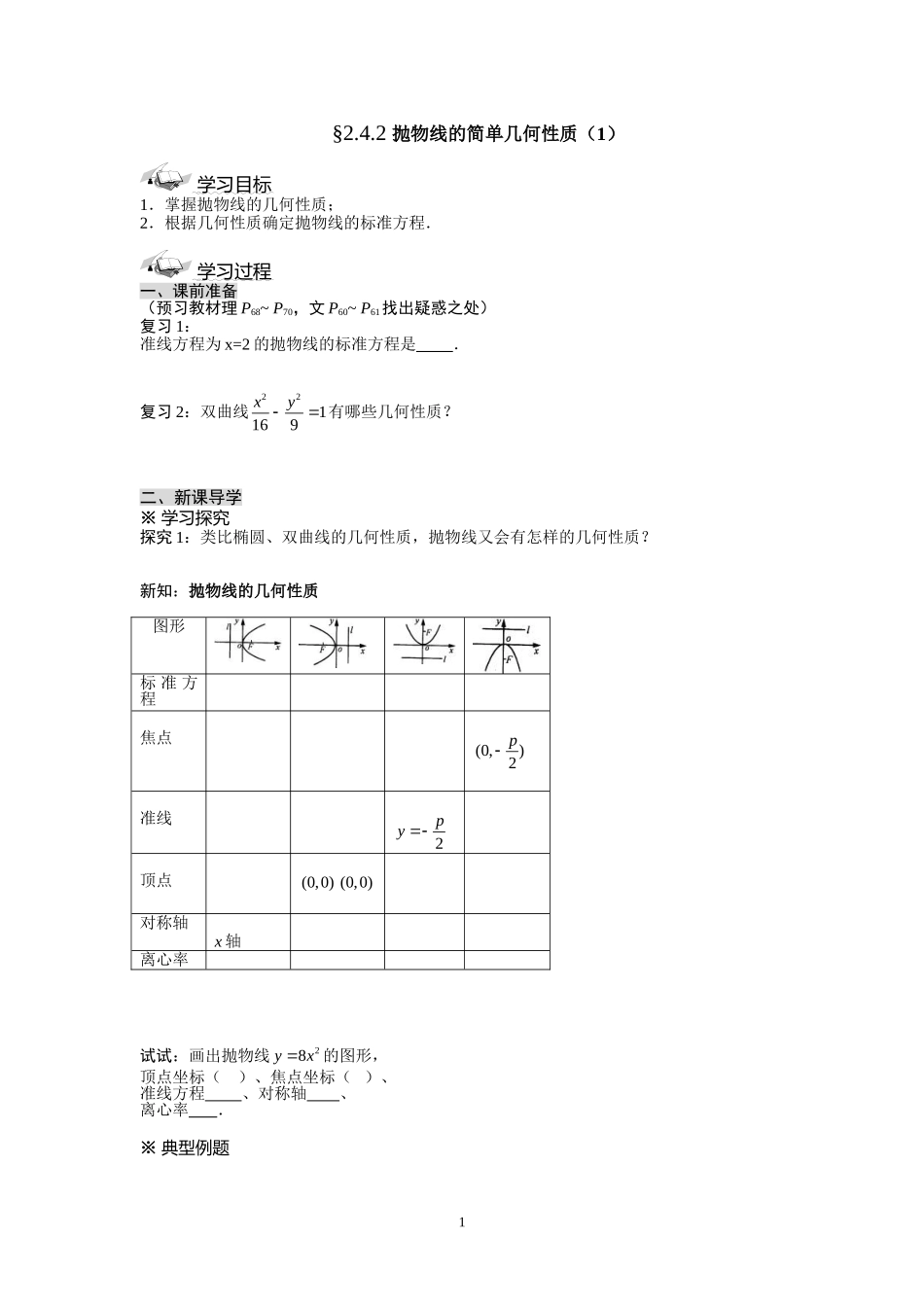
§2.4.2抛物线的简单几何性质（1）学习目标1．掌握抛物线的几何性质；2．根据几何性质确定抛物线的标准方程．学习过程一、课前准备（预习教材理P68~P70，文P60~P61找出疑惑之处）复习1：准线方程为x=2的抛物线的标准方程是．复习2：双曲线221169xy有哪些几何性质？二、新课导学※学习探究探究1：类比椭圆、双曲线的几何性质，抛物线又会有怎样的几何性质？新知：抛物线的几何性质图形标准方程焦点(0,)2p准线2py顶点(0,0)(0,0)对称轴x轴离心率试试：画出抛物线28yx的图形，顶点坐标（）、焦点坐标（）、准线方程、对称轴、离心率．※典型例题1例1已知抛物线关于x轴对称，它的顶点在坐标原点，并且经过点(2,22)M，求它的标准方程．变式：顶点在坐标原点，对称轴是坐标轴，并且经过点(2,22)M的抛物线有几条？求出它们的标准方程．小结：一般，过一点的抛物线会有两条，根据其开口方向，用待定系数法求解．例2斜率为1的直线l经过抛物线24yx的焦点F，且与抛物线相交于A，B两点，求线段AB的长．变式：过点(2,0)M作斜率为1的直线l，交抛物线24yx于A，B两点，求AB．2小结：求过抛物线焦点的弦长：可用弦长公式，也可利用抛物线的定义求解．※动手试试练1.求适合下列条件的抛物线的标准方程：⑴顶点在原点，关于x轴对称，并且经过点(5M，4)；⑵顶点在原点，焦点是(0,5)F；⑶焦点是(0,8)F，准线是8y．三、总结提升※学习小结1．抛物线的几何性质；2．求过一点的抛物线方程；3．求抛物线的弦长．※知识拓展抛物线的通径：过抛物线的焦点且与对称轴垂直的直线，与抛物线相交所得的弦叫抛物线的通径．其长为2p．学习评价※自我评价你完成本节导学案的情况为（）.A.很好B.较好C.一般D.较差※当堂检测（时量：5分钟满分：10分）计分：1．下列抛物线中，开口最大的是（）．A．212yxB．2yxC．22yxD．24yx2．顶点在原点，焦点是(0,5)F的抛物线方程（）．A．220yxB．220xyC．2120yxD．2120xy33．过抛物线24yx的焦点作直线l，交抛物线于A，B两点，若线段AB中点的横坐标为3，则AB等于（）．A．10B．8C．6D．44．抛物线2(0)yaxa的准线方程是．5．过抛物线22yx的焦点作直线交抛物线于11(,)Axy，22(,)Bxy两点，如果126xx，则AB=．课后作业1．根据下列条件，求抛物线的标准方程，并画出图形：⑴顶点在原点，对称轴是x轴，并且顶点与焦点的距离等到于6；⑵顶点在原点，对称轴是y轴，并且经过点(6,3)P．2M是抛物线24yx上一点，F是抛物线的焦点，60xFM，求FA．4