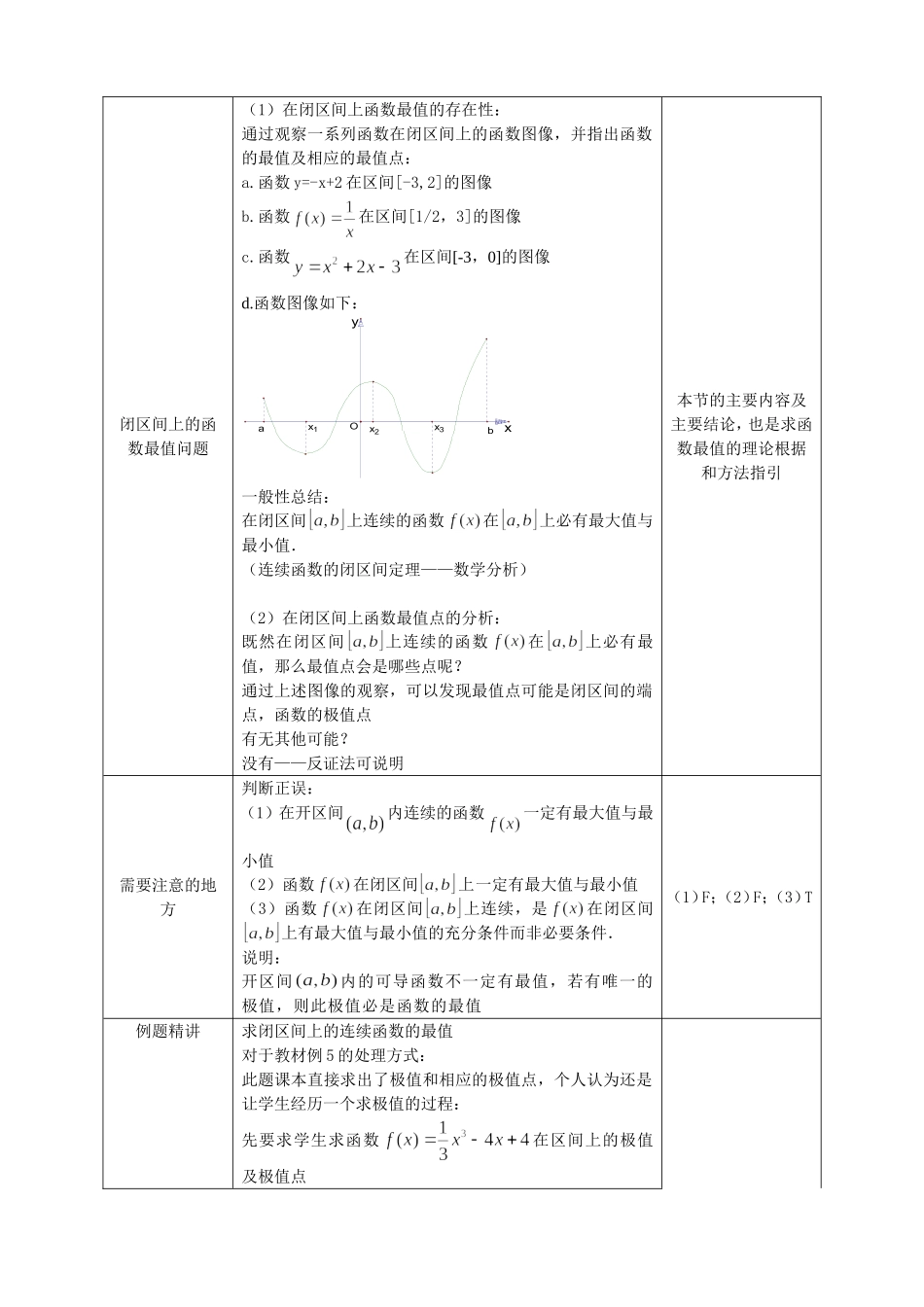
§1.3.3函数的最大(小)值与导数(1课时)【学情分析】:这部分是在高一学过的函数单调性的基础上,给出判定可导函数增减性的方法,然后讨论函数的极值,由极值的意义,结合图象,得到利用导数判别可导函数极值的方法,最后在可以确定函数极值的前提下,给出求可导函数的最大值与最小值的方法【教学目标】:(1)使学生理解函数的最大值和最小值的概念,能区分最值与极值的概念(2)使学生掌握用导数求函数最值的方法和步骤【教学重点】:利用导数求函数的最大值和最小值的方法.【教学难点】:函数的最大值、最小值与函数的极大值和极小值的区别与联系.熟练计算函数最值的步骤【教学过程设计】:教学环节教学活动设计意图复习引入设函数f(x)在点x0附近有定义,f(x0)是函数f(x)的一个极大值f(x0),x0是极大值点,则对x0附近的所有的点,都有f(x)____f(x0)设函数f(x)在点x0附近有定义,f(x0)是函数f(x)的一个极小值f(x0),x0是极小值点,则对x0附近的所有的点,都有f(x)____f(x0)知识的巩固概念对比回顾以前所学关于最值的概念,形成对比认识:函数最大值的概念:设函数y=f(x)的定义域为I.如果存在实数M满足:(1)对于任意的_____,都有f(x)___M(2)存在__________,使得_______则称M为函数y=f(x)的最________值函数最小值的概念:设函数y=f(x)的定义域为I.如果存在实数M满足:(1)对于任意的_____,都有f(x)___M(2)存在__________,使得_______则称M为函数y=f(x)的最________值思考:你觉得极值与最值的区别在哪里?让学生发现极值与最值的概念区别,概念辨析练习(1)函数的极大(小)值一定是函数的最大(小)值,极大(小)值点就是最大(小)值点(2)函数的最大(小)值一定是函数的极大(小)值,最大(小)值点就是极大(小)值点(3)函数y=f(x)在x=a处取得极值是函数y=f(x)在x=a处取得最值的____________(充要性)通过练习深化他们对函数取极值与最值的区别对极值与最值概念的深化理解(1)函数的最值是比较整个定义域内的函数值得出的;函数的极值是比较极值点附近函数值得出的.(2)函数的最值是描述函数在整个定义域上的整体性质,函数的极值是描述函数在某个局部的性质(3)函数在其定义区间上的最大值、最小值最多各有一个,而函数的极值可能不止一个,也可能没有一个点评提高闭区间上的函数最值问题(1)在闭区间上函数最值的存在性:通过观察一系列函数在闭区间上的函数图像,并指出函数的最值及相应的最值点:a.函数y=...