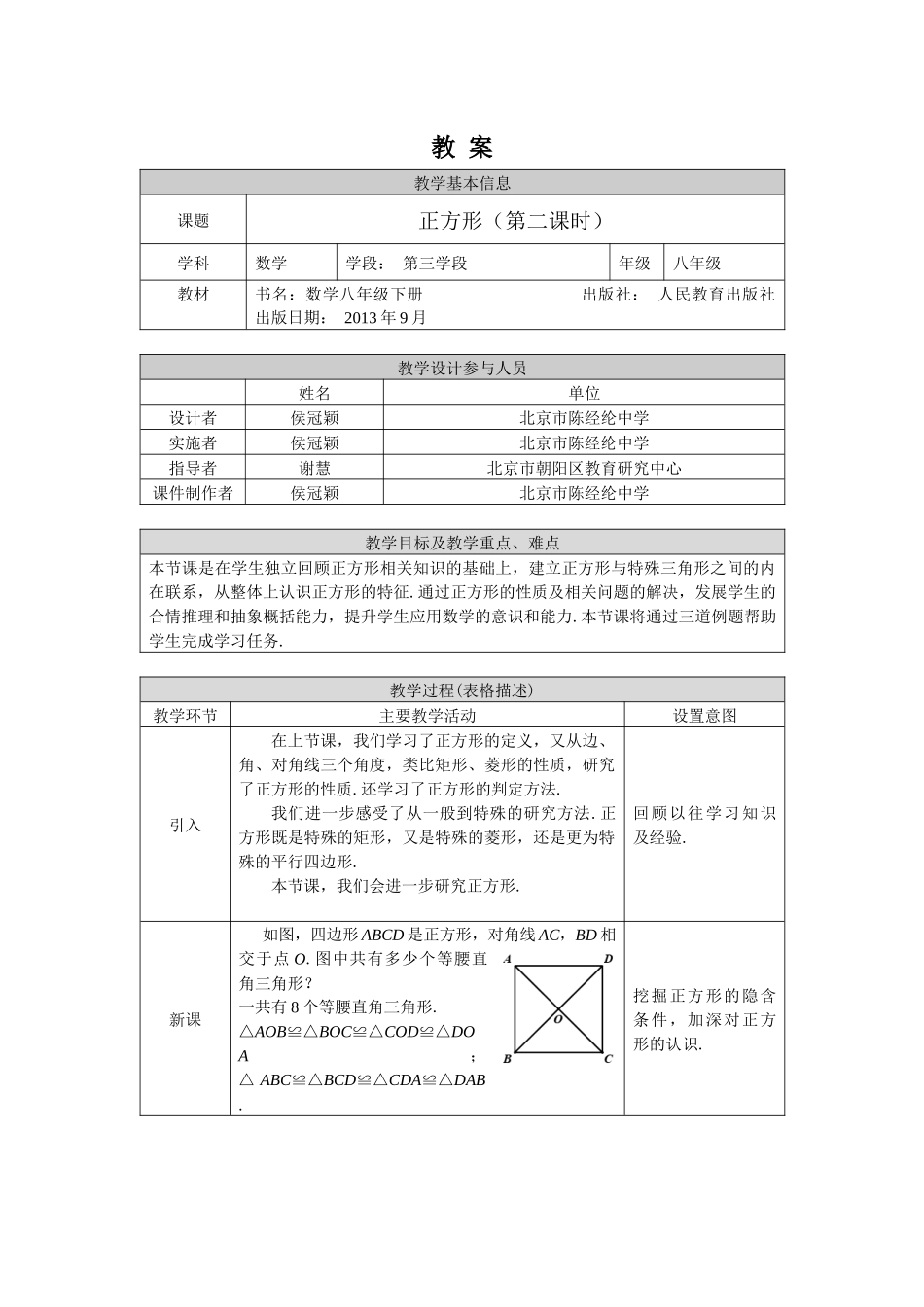
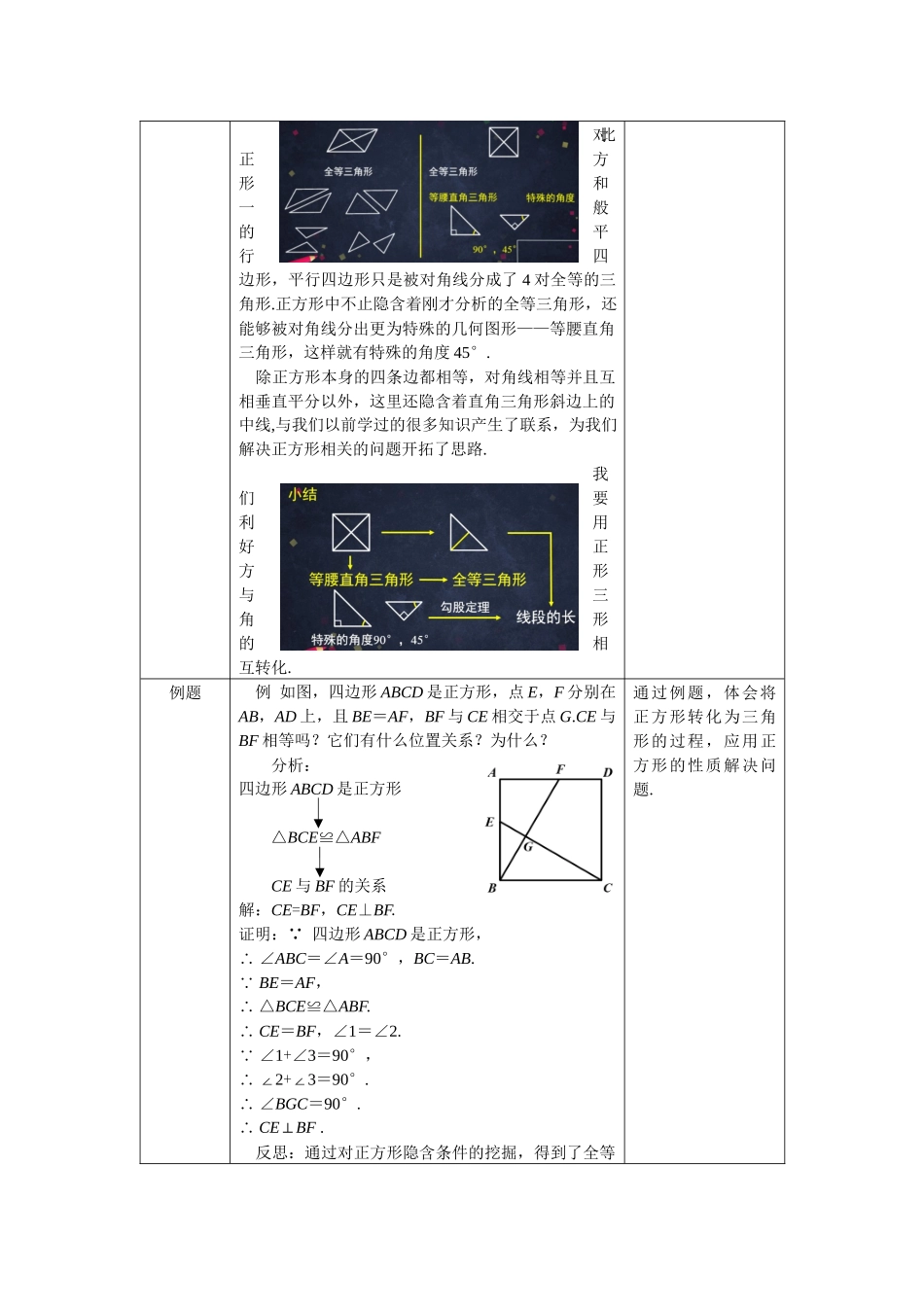
教案教学基本信息课题正方形(第二课时)学科数学学段:第三学段年级八年级教材书名:数学八年级下册出版社:人民教育出版社出版日期:2013年9月教学设计参与人员姓名单位设计者侯冠颖北京市陈经纶中学实施者侯冠颖北京市陈经纶中学指导者谢慧北京市朝阳区教育研究中心课件制作者侯冠颖北京市陈经纶中学教学目标及教学重点、难点本节课是在学生独立回顾正方形相关知识的基础上,建立正方形与特殊三角形之间的内在联系,从整体上认识正方形的特征.通过正方形的性质及相关问题的解决,发展学生的合情推理和抽象概括能力,提升学生应用数学的意识和能力.本节课将通过三道例题帮助学生完成学习任务.教学过程(表格描述)教学环节主要教学活动设置意图引入在上节课,我们学习了正方形的定义,又从边、角、对角线三个角度,类比矩形、菱形的性质,研究了正方形的性质.还学习了正方形的判定方法.我们进一步感受了从一般到特殊的研究方法.正方形既是特殊的矩形,又是特殊的菱形,还是更为特殊的平行四边形.本节课,我们会进一步研究正方形.回顾以往学习知识及经验.新课如图,四边形ABCD是正方形,对角线AC,BD相交于点O.图中共有多少个等腰直角三角形?一共有8个等腰直角三角形.△AOB≌△BOC≌△COD≌△DOA;△ABC≌△BCD≌△CDA≌△DAB.挖掘正方形的隐含条件,加深对正方形的认识.对比正方形和一般的平行四边形,平行四边形只是被对角线分成了4对全等的三角形.正方形中不止隐含着刚才分析的全等三角形,还能够被对角线分出更为特殊的几何图形——等腰直角三角形,这样就有特殊的角度45°.除正方形本身的四条边都相等,对角线相等并且互相垂直平分以外,这里还隐含着直角三角形斜边上的中线,与我们以前学过的很多知识产生了联系,为我们解决正方形相关的问题开拓了思路.我们要利用好正方形与三角形的相互转化.例题例如图,四边形ABCD是正方形,点E,F分别在AB,AD上,且BE=AF,BF与CE相交于点G.CE与BF相等吗?它们有什么位置关系?为什么?分析:四边形ABCD是正方形△BCE≌△ABFCE与BF的关系解:CE=BF,CE⊥BF.证明: 四边形ABCD是正方形,∴∠ABC=∠A=90°,BC=AB. BE=AF,∴△BCE≌△ABF.∴CE=BF,∠1=∠2. ∠1+∠3=90°,∴∠2+∠3=90°.∴∠BGC=90°.∴CE⊥BF.反思:通过对正方形隐含条件的挖掘,得到了全等通过例题,体会将正方形转化为三角形的过程,应用正方形的性质解决问题.三角形,根据全等三角形的性质,得到对应边相等对应角相等.在...